Лекция 21. Формула Тейлора

Если дифференциал функции описывает приращение функции в первом приближении, то многочлен Тейлора описывает при­ращение функции со сколь угодной точностью.

Задача 1

Пусть функция ¦(x) непрерывна и сколь угодное число раз дифференцируема на отрезке [a, b]. Найти эквивалентную при­ращения функции в точке x₀ Î (а, b) в виде многочлена n-ой степени.

Ø Согласно предыдущей лекции

Итак, приращение функции в точке x₀, в виде многочлена n -ой степени имеет вид

где второе слагаемое дает погрешность многочлена Тейлора. Тоже равенство можно записать иначе

Задача 2

Пусть функция f(x) непрерывна и сколь угодное число раз дифференцируема в окрестности точки x = 0. Представить её в виде многочлена n -ой степени в окрестности этой точки.

· Согласно Задачи 1

Поскольку все последующие производные равны нулю, то под­становка производных в формулу Маклорена даст точное равенство

Полученный результат можно записать иначе

Пример 3. Известно, что sin x 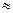х.

x 0

Найти следующее приближение.