Замечания

1. Оценка (4.23) для линейной интерполяции инвариантна по отношению к виду сетки 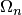(равномерной или неравномерной). Параболическая интерполяция также сохраняет указанную погрешность при выполнении интерполяции на неравномерной сетке 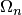. В некоторых источниках для 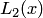при выполнении условия 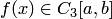приведена оценка

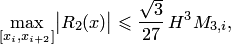
(4.25)

где.

2. Если гладкость функции 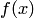не достигает вышеуказанной и класс гладкости понижен на единицу 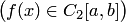, то порядок параболической интерполяции также понижается на единицу:

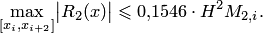
(4.26)

3. Повышение класса гладкости функции 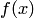выше 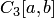не приводит к увеличению порядка параболической интерполяции относительно Н, т.е. происходит как бы его "замораживание" или "насыщение". Указанные свойства, вытекающие из оценок (4.25), (4.26), носят общий характер и имеют место в других оценках аппроксимации многочленов, сплайнов, производных и интегралов.

4. Для произвольной степени интерполяционного многочлена при 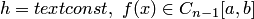погрешность функциональной интерполяции на отрезке 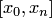выражается следующим образом:

(4.27)

где. Для многочленов с 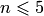величины 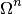или их оценки являются такими:

Из (4.27) следует, что на отрезке 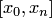величина 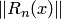есть 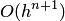и при уменьшении шага 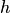в два раза мажоранта уменьшается по крайней мере в 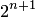раз. Отсюда вытекает, что для непрерывных функций можно по заданной точности интерполяции выбирать шаг 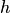. При этом можно путем использования кусочной интерполяции в некоторых пределах изменять степень интерполяционного многочлена. Мажоранту в оценке (4.27) при кусочной интерполяции можно также снизить путем выбора "окна" интерполяции 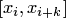так, чтобы точка 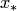располагалась как можно ближе к его середине. Это обусловлено тем, что колебания функции 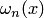вблизи середины 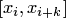меньше, чем у его концов.

5. В широком классе задач математической физики применяются расчетные схемы в основном второго (и иногда третьего и выше) порядка точности. При их реализации, как правило, используются встроенные интерполяционные алгоритмы, основанные на многочленах и сплайн-функциях. Степени интерполяционных многочленов при этом должны выбираться из условия соответствия порядков их аппроксимации порядкам точности схем. Если эти порядки одинаковы, то порядок точности схем сохраняется, хотя константа в оценке погрешности схемы изменяется. Если же порядок встроенных интерполяционных алгоритмов хотя бы на единицу выше порядка точности схемы, то вместе с порядком точности схемы сохраняется и указанная константа. Отсюда следует, что необходимо выбирать такую степень интерполяционного многочлена, которая либо обеспечивает равенство порядка аппроксимации порядку точности схемы, либо на единицу превышает последний. Таким образом, использование параболической интерполяции в качестве встроенных алгоритмов или для восполнения численных решений, полученных по схемам второго порядка, позволяет сохранить требуемую точность расчета, а также не дает избыточный порядок и, следовательно, не усложняет алгоритм. Это замечание носит общий характер и относится к любым аппроксимационным алгоритмам, выполняющим функцию восполнения или интерполирования.