Тема 12.4. Однорідні ЛДР (ОЛДР) зі сталими коефіцієнтами.
Неоднорідні ЛДР (НЛДР). Метод варіації довільних сталих. Визначення частинного розв'язку НЛДР з правою частиною спеціального вигляду 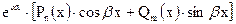 .
.
ВПРАВИ.
1. Розв’язати неоднорідні лінійні диф. рівняння з постійними коефіцієнтами.
а) Знайти частинний розв’язок: 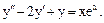 у(0)=1,
у(0)=1, 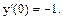
Розв’язання. Загальний розв’язок має вигляд 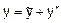 , де
, де 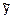 - загальний розв’язок відповідного однорідного рівняння
- загальний розв’язок відповідного однорідного рівняння 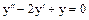 ,
, 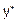 - який-небудь частинний розв’язок даного неоднорідного рівняння.
- який-небудь частинний розв’язок даного неоднорідного рівняння.
Знаходження 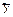 за допомогою характеристичного рівняння
за допомогою характеристичного рівняння
r2-2r+1=0. В цьому випадку однакових коренів 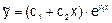 =
=
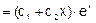 ,
, 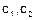 – довільні сталі.
– довільні сталі.
Знаходження 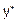 . Права частина рівняння має вигляд
. Права частина рівняння має вигляд 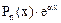 , де Рn(х)=х,
, де Рn(х)=х, 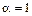 .
. 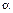 співпадає з обома коренями r1=r2=1. В цьому випадку
співпадає з обома коренями r1=r2=1. В цьому випадку 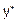 шукають у вигляді
шукають у вигляді 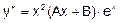 , знаходячи А і В
, знаходячи А і В
підстановкою 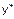 у дане диф. рівняння:
у дане диф. рівняння: 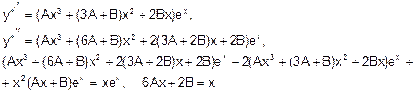
Коефіцієнти при однакових степенях х рівних многочленів рівні, тоді:
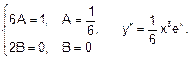
Загальний розв’язок: 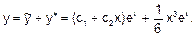
Із початкової умови знаходять с1, с2: 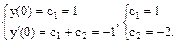
Частинний розв’язок: 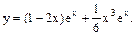
б) Знайти загальний розв’язок: 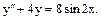
Розв’язання. 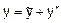 . Знаходження
. Знаходження 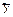 :
:
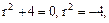
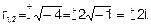
В цьому випадку комплексних коренів 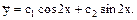
Знаходження 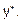 Права частина рівняння має вигляд
Права частина рівняння має вигляд
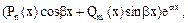 де
де 
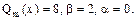
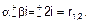 В цьому випадку
В цьому випадку 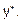 шукають у вигляді
шукають у вигляді
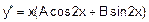 .
.
Підстановка в диф. рівняння:
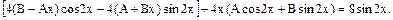
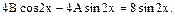
Із умови рівності коефіціентів справа і зліва: при sin2x -4A=8, A = - 2, при cos2x 4B=0, B = 0. 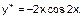
Загальний розв’язок 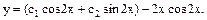
 2015-08-21
2015-08-21 406
406








