Тема 12.2. ЗДР 1-го порядку в несиметричній та симетричній формах: з відокремленими та з відокремлюваними змінними, однорідні, лінійні та Бернуллі. ЗДР у повних диференціалах. Задача Коші.
ВПРАВИ.
1. Розв’язати диференціальні рівняння першого порядку.
а) Знайти загальний розв’язок, 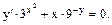
Розв’язання. Дане рівняння- рівняння з відокремлюваними змінними.
Відокремлення змінних: 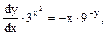
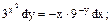
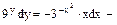 змінні відокремлені.
змінні відокремлені.
Інтегрування: 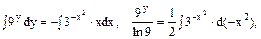
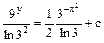 - загальний розв’язок, с- довільна стала.
- загальний розв’язок, с- довільна стала.
Спрощення: 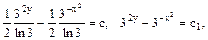 де
де 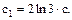
Відповідь: 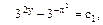
б) Знайти загальний розв’язок, 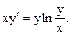
Розв’язання. Дане рівняння однорідне. Дійсно, після приведення його до вигляду 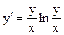 праворуч однорідна функція степені нуль:
праворуч однорідна функція степені нуль:
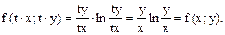
Введення нової невідомої функції z(x): 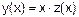
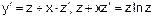 - це рівняння з відокремлюваними змінними.
- це рівняння з відокремлюваними змінними.
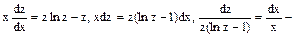 це рівняння еквівалентне вихідному при
це рівняння еквівалентне вихідному при 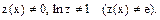
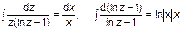 ,
, 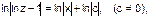
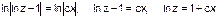 ,
, 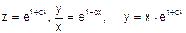 - це загальний розвязок.
- це загальний розвязок.
Перевірка можливих загублених через використані обмеження розв’язків: z=0, 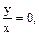 y=0 - точки (х;0) не входять в область означення рівняння; z=e, y=xe - підстановка у вихідне рівняння дає тотожність хе=хе, це означає, що у=хе - додатковий розв’язок.
y=0 - точки (х;0) не входять в область означення рівняння; z=e, y=xe - підстановка у вихідне рівняння дає тотожність хе=хе, це означає, що у=хе - додатковий розв’язок.
Розв’язок рівняння: 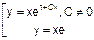 .
. 

Можна об’єднати обидві функції: 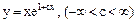 - це відповідь.
- це відповідь.
в) Знайти частинний розв’язок рівняння 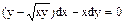 з початковою умовою у(1)=4.
з початковою умовою у(1)=4.
Розв’язання. Дане рівняння-однорідне в симетричній формі. Дійсно функції М(х,у)= 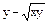 , N(x,y)= - x однорідні однакової (першої) степені, рівняння приводиться до вигляду
, N(x,y)= - x однорідні однакової (першої) степені, рівняння приводиться до вигляду 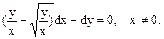
Введення нової змінної z: y=xz, dy=zdx+xdz.
Підстановка в диф. рівняння: (z- 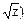 dx - (zdx+xdz)=0, -
dx - (zdx+xdz)=0, - 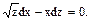
Відокремлення змінних: 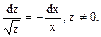
Інтегрування: 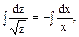
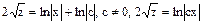 -загальний розвязок при
-загальний розвязок при 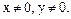
Із початкових умов: 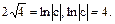
Частинний розв’язок: 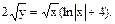
г) Знайти розв’язок задачі Коши 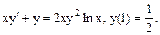
Розв’язання. Дане рівняння- це рівняння Бернуллі. Розв’язується методом Бернуллі. Невідому функцію шукають у вигляді 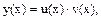 тоді
тоді 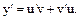
Підстановка в диф. рівняння: 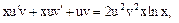
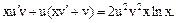 . Добирають
. Добирають 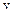 так, щоб
так, щоб 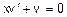
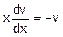 ,
, 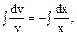
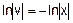 ,
, 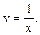
Знаходять u: 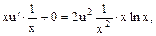
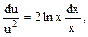
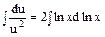 ,
, 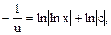
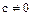 ,
, 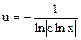 .
.
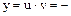
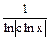 - загальний розв’язок.
- загальний розв’язок.
Із початкової умови 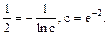
Частинний розв’язок: 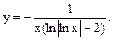
д) Знайти загальний розв’язок, 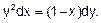
Розв’язання. Дане диф. рівняння лінійне відносно функції х=х(у). Дійсно, воно зводиться до рівняння в несиметричній формі 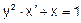 .
.
Розв’язання методом Бернуллі: 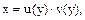
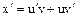 ,
, 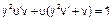 ,
, 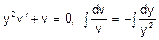 ,
, 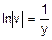 ,
, 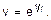
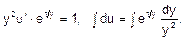
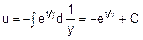 .
.
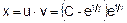 . Відповідь
. Відповідь 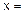
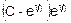 .
.
є) Знайти загальний розв’язок: 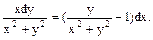
Розв’язання. Дане рівняння–це рівняння у повних диференціалах: воно задовольняє необхідній і достатній умові таких рівнянь 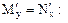
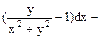
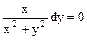 ,
, 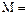
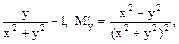
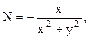
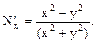
Інтеграл рівняння у повних диференціалах (тобто функція u(x;y) така, що du(x;y)=M(x,y)dx+N(x,y)dy) шукають за допомогою криволінійного інтеграла: 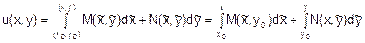
або 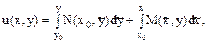
де (х0,у0)- деяка початкова точка, шлях інтегрування – ломана, яка складається з відрізків паралельних координатним вісям і не включає точок, в яких M=N=0. Нехай х0=0, у0=1, тоді
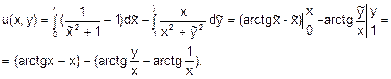
Загальний розв’язок представляється у вигляді загального інтеграла
u(x,y)=c: 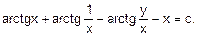
 2015-08-21
2015-08-21 324
324








