2015-08-21
393
Тема 13.1 Числові ряди. Безпосереднє дослідження, необхідна умова збіжності.
Достатні умови збіжності знакододатних рядів: порівняння, Даламбера, радикальні та інтегральна Коші.
Знакозмінні ряди абсолютно та умовно збіжні. Знакопочережні (знакопереміжні) ряди, теорема Лейбниця. 4 4 2
ВПРАВИ
1. Дослідити числові ряди.
а)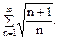 
Розв’язання. Застосування висновку необхідної умови збіжності числового ряду:
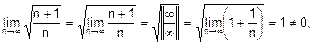ряд розбіжний.
б)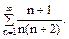 
Розв’язання. Ряд знакододатний.
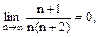тож необхідна умова збіжності не заперечує збіжності ряду. Треба скористатись достатніми умовами збіжності. Загальний член даного ряду – раціональний дріб, який має порядок 
̃~ 
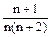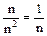при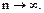 
В цьому випадку застосовують ознаки порівняння,- порівняння з гармонічним розбіжним рядом 
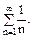За другою ознакою порівняння 
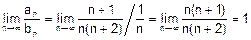скінченна ненульова границя, тож даний ряд, як і гармонічний ряд, розбіжний.
в)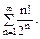 
Розв’язання. Ряд знакодатний. Якщо загальний член складається з факторіалів і показникових функцій, то зручна ознака Даламбера:
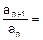
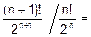
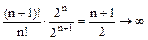
це необмежена функція при n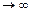 
, ряд розбіжний.
г)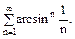 
Розв’язання. Загальний член ряду-степенево показникова функція. В цьому випадку зручна радикальна ознака Коши:
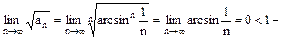ряд збіжний.
д)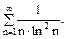 
Розв’язання. Ряд знакодатний. У випадках, коли застосування інших ознак укладнене, може бути зручною інтегральна ознака збіжності: нехай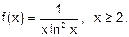 
,
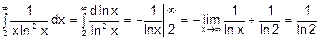невластивий інтеграл збіжний, тож і ряд збіжний.
є)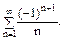 
Розв’язання. Ряд знакозмінний. Тому треба з’ясувати не тільки його збіжність, але і характер збіжності - абсолютний чи умовний. Спочатку досліджується абсолютна збіжність: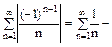 
знакододатний гармонічний ряд, відомо, що він розбіжний, і тому даний ряд не є абсолютно збіжним і треба дослідити його ще і на умовну збіжність.
Ряд знакопочережний. Перевіряють умови ознаки Лейбниця:
1) 
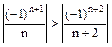або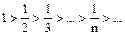 
2) 
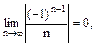
умови виконуються, ряд збігається умовно.
