Методы Оптимизации
Общая постановка задачи математического программирования.
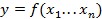
Найти наибольшее и наименьшее значения y при ограничениях:
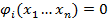 , i=1,2,…,k;
, i=1,2,…,k;
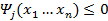 , j=1,2,…,l;
, j=1,2,…,l;
Ограничения бывают типа равенств и неравенств.
Метод неопределенных множителей Лагранжа при поиске максимальных значений функций.
Найти экстремальные значения y при наличии ограничений типа равенств:
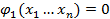

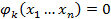
1) Образуем функцию Φ.
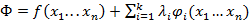 от n+k – переменных.
от n+k – переменных.
2) Ищем экстремум функции Ф.
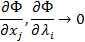
3) Пусть M 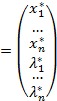 - точка установленного экстремума,
- точка установленного экстремума,
тогда М*= 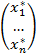 - точка установленного экстремума функции Ф.
- точка установленного экстремума функции Ф.

2 этапа решения задач:
1) ищется условие оптимальности
2) технический этап – решение уравнений
1-ый способ общий, 2-ой не всегда реализуем.
Линейный функционал.
Переменная величина I называется функционалом, зависящим от функции y=y(x), что обозначается так: 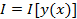 , если каждой функции
, если каждой функции 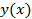 из некоторого класса функций
из некоторого класса функций 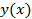 соответствует значение I, т.е. имеет место соответствие: функции
соответствует значение I, т.е. имеет место соответствие: функции 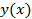 соответствует число I.
соответствует число I.
Линейным функционалом называется функционал 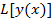 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) 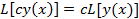 , где с – произвольная постоянная
, где с – произвольная постоянная
2) 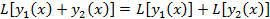
 2015-08-21
2015-08-21 403
403







