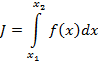
Порядок вычисления вариации функционала:
1. Заменяем аргумент: 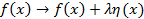 , где
, где 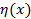 – вариация аргумента;
– вариация аргумента;
2. Вычисляем частную производную по 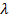 ;
;
3. В полученном выражении полагаем 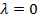 , находим вариацию функционала
, находим вариацию функционала 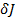
6) Постановка задачи Эйлера.
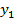
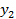
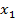
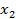
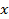
Задача – провести через две точки оптимальную кривую. В задаче Эйлера формируется критерий оптимальности: 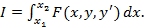
Для задания критерия выбираем функцию от трех вещественных аргументов: 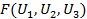 или
или 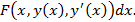 Выполнив преобразования аргументов, получим функцию от одного вещественного аргумента.
Выполнив преобразования аргументов, получим функцию от одного вещественного аргумента.
Итак, нужно выбрать такую кривую, которая является экстремумом от функционала.
Условие экстремума: одинаковый знак приращения при изменении аргумента, т.е. 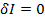 .
.
 2015-08-21
2015-08-21 1086
1086








