Электромеханические преобразователи электромагнитного типа состоят из электромагнита и механического узла (см. рис. 1.68).
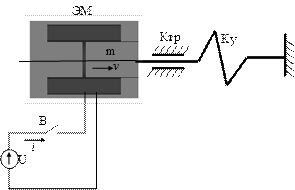
Рис. 1.68. Схема электромеханического преобразователя электромагнитного типа.
Преобразование электрической энергии в электромагнитную и затем в механическую или в обратной последовательности осуществляется за счет подвижного якоря, составляющего часть сердечника электромагнита. Якорь намагничивается в магнитном поле электромагнита и возникают силы взаимодействия намагниченного тела с магнитным полем, в которое оно помещено. Анализ процессов преобразования энергии состоит в определении зависимостей тока в катушке электромагнита, скорости и перемещения якоря, параметров движения механического узла от времени в переходных и установившихся режимах. Механическая нагрузка преобразователя представляется кинематической схемой с элементами трения, пружинам, инерционными элементами (массами, моментами инерции тел) и источниками внешних сил и моментов.
Модель такой электромеханической системы можно построить, используя следующую методику решения задачи: модели со сосредоточенными параметрами в виде электрических цепей применяются для электрической и механической подсистем [4], а анализ магнитной подсистемы выполняется с помощью численного анализа магнитного поля.
Эквивалентная схема электрической цепи для изображенного на рис. 1.68 преобразователя содержит источник постоянной ЭДС – U, Выключатель В, активное сопротивление провода катушки и индуцируемую в катушке ЭДС – e(t) (см. рис. 1.69, а), которая согласно закону электромагнитной индукции определяется взятой со знаком минус производной потокосцепления катушки 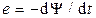 .
.
Эквивалентная схема механической подсистемы (см. рис. 1.69, б) в соответствии с кинематической схемой на рис. 1.68 составлена из источника силы P (аналог источника тока в электрической цепи), резистора с сопротивлением 1 /К тр, представляющего вязкое трение, индуктивности со значением 1 /К у – модели пружины и конденсатора с емкостью m – масса подвижной части преобразователя (якоря, штока и пр.). Скорость якоря v в модели определена напряжением на конденсаторе.
Система дифференциальных уравнений, записанная для анализа динамики работы системы, имеет вид:
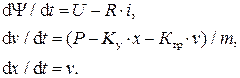
В программной среды Matlab Simulink расчетные уравнения формируются автоматически по составленным эквивалентным схемам.
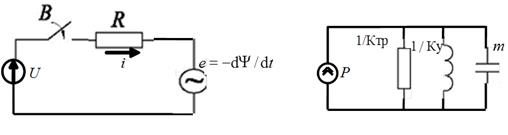
а) б)
Рис. 1.69. Эквивалентные схемы электрической и механической подсистем: а - электрическая подсистема; б – механическая подсистема.
Эта система уравнений не замкнута, так как не определена связь потокосцепления с остальными параметрами или ее временная функция. Для решения задачи используют итерационные пошаговые алгоритмы расчета электромагнитного поля в существующих пакетах программ для расчета полей [10, 4]. Однако здесь могут возникнуть трудности из-за разномасштабности во времени электромагнитных и механических процессов, что вызовет недопустимое возрастание объема и требуемого времени вычислений.
Для упрощения задачи принимают допущения об отсутствии индуцированных токов и магнитного гистерезиса в магнитопроводе и якоре электромагнита. В этом случае потокосцепление катушки и электромагнитную силу можно представить зависимостями только от двух переменных: перемещения x и тока i: 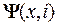 и
и 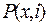 . Такие зависимости в табличной форме или в виде аппроксимирующих функций определяются расчетом электромагнитного поля в выбранном диапазоне варьирования переменных
. Такие зависимости в табличной форме или в виде аппроксимирующих функций определяются расчетом электромагнитного поля в выбранном диапазоне варьирования переменных 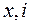 .
.
Связь между электрической и механической подсистемами на рис. 1.69 задается через источники фазовых переменных: индуцируемой в катушке электромагнита ЭДС и электромагнитную силу. Предположим были рассчитаны эти функции и аппроксимированы полиномами:
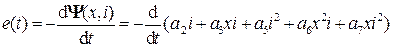 ,
,
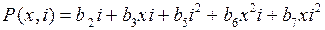 .
.
Модель электромеханического преобразователя электромагнитного типа, в которую включены аппроксимирующие функции потокосцепления и силы, представлена в программной среде Matlab Simulink на рис. 1.70. В схему включен генератор импульсов для управления выключателем электромагнита.
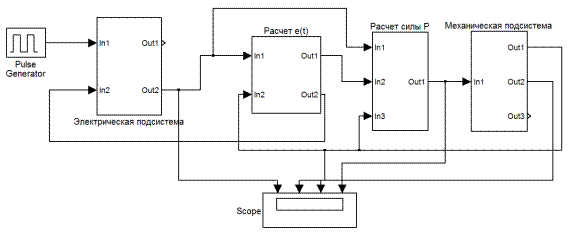
Рис. 1.70. Модель электромеханического преобразователя электромагнитного типа в Matlab Simulink.
Электрическая подсистема модели (рис. 1.71) составлена из источника постоянного напряжения U, выключателя В, сопротивления провода катушки R и индуцируемой в катушке ЭДС 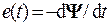 , моделируемой управляемым источником напряжения. В схему включен амперметр А.
, моделируемой управляемым источником напряжения. В схему включен амперметр А.
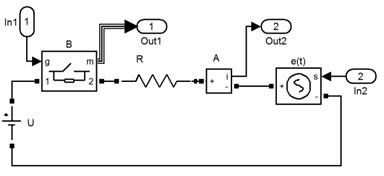
Рис. 1.71. Модель электрической подсистемы.
Расчет индуцируемой в катушке электромагнита ЭДС выполнен по схеме рис. 1.72, а. На вход In1 подается текущее значение тока из электрической подсистемы, а на вход In2 - значение перемещения якоря из механической подсистемы. На выходе Out2 формируется значение e(t), а на выходе Out1 – сигнал квадрата тока 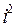 , который далее используется для расчета силы. Выход Out2 соединен с управляемым источником напряжения в электрической подсистеме.
, который далее используется для расчета силы. Выход Out2 соединен с управляемым источником напряжения в электрической подсистеме.
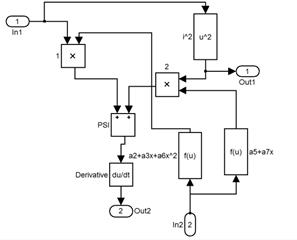
Расчет сил по построенному полиному производится по схеме рис. 1.72, б. На вход In1 подается текущее значение тока из электрической подсистемы, вход In2 - значение квадрата тока из блока расчета ЭДС, а на вход In3 - перемещения якоря из механической подсистемы. На выходе Out1 формируется сигнал силы, который управляет источником силы в механической подсистеме.
 а) а) | 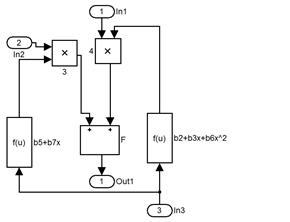 б) б) |
Рис. 1.72. Модели расчета управляющих сигналов: а – расчет индуцируемой ЭДС e(t); б – расчета силы P.
Схема механической подсистемы представлена на рис. 1.73. Сила, действующая на якорь, моделируется управляемым источником тока, у которого на вход In1 подается управляющий сигнал из блока расчета силы. Вязкое трение, пружина и масса подвижной части устройства представлены соответственно резистором, индуктивностью и конденсатором.
Рис. 1.73. Модель механической подсистемы.
В модель включен упор, ограничивающий перемещение якоря в промежутке 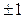 мм. Модель упора представляет собой шунтирующую цепь из RL - элементов – упругая стенка с рассеянием энергии. Когда якорь касается упора, замыкается ключ и подключается шунтирующая цепь. Для расчета перемещения якоря построена логическая цепь: вольтметр V2 дает значение скорости якоря. После интегратора получаем значение перемещения в метрах, которое затем пересчитывается в миллиметры, так как в функциональных блоках приняты такие единицы измерения. Начальное положение якоря задает элемент Constant. Пределы перемещения якоря – упоры, определены элементом Relay
мм. Модель упора представляет собой шунтирующую цепь из RL - элементов – упругая стенка с рассеянием энергии. Когда якорь касается упора, замыкается ключ и подключается шунтирующая цепь. Для расчета перемещения якоря построена логическая цепь: вольтметр V2 дает значение скорости якоря. После интегратора получаем значение перемещения в метрах, которое затем пересчитывается в миллиметры, так как в функциональных блоках приняты такие единицы измерения. Начальное положение якоря задает элемент Constant. Пределы перемещения якоря – упоры, определены элементом Relay
В качестве характерного примера приведем результаты расчетов изображенной на рис. 1.68 системы, в которой применен цилиндрический электромагнит броневого типа с размерами, указанными на рис. 1.74.
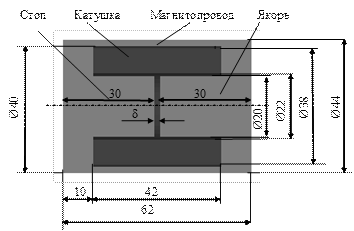
Рис. 1.74. Цилиндрический электромагнит броневого типа.
Задача состояла в построении зависимостей тока i, скорости v и перемещения x от времени в электромеханической системе при включении электромагнита на источник постоянного напряжения U. Механическая нагрузка представлена элементами вязкого трения с коэффициентом К тр, пружиной с жесткостью К у и массой подвижной части m. Перемещение линейное по оси x.
Исходные данные: U = 2.4 В; m = 0.5 кг; К тр=0.001 кг/с; К у=1000 Н/м; сопротивление провода R пр=0.2 Ом; число витков катушки N = 40; материал магнитопровода и якоря – сталь 10.
Начальные условия при анализе процесса включения электромагнита: зазор – δ= x 0 =2 мм; сила начального поджатия пружины P пр0=-2 Н; начальная скорость v =0.
Рассчитанные с помощью программы анализа электромагнитного поля зависимости потокосцепления катушки и силы от перемещения якоря при различных токах приведены на рис. 1.75, 1.76.
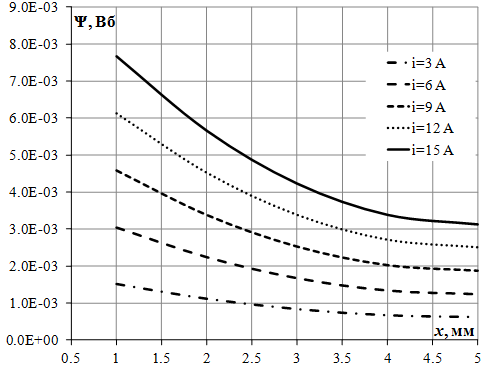
Рис. 1.75. Зависимость потокосцепления катушки электромагнита от перемещения якоря (зазора) при различных токах.
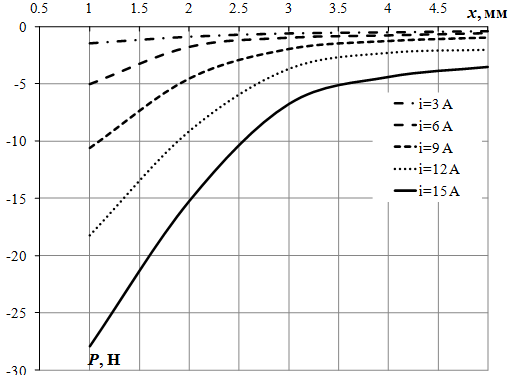
Рис. 1.76. Зависимость силы, действующей на якорь электромагнита от перемещения якоря (зазора) при различных токах.
Результаты расчетов динамики работы электромеханической системы представлены на рис. 1.77. В начале процесса источник питания выключен и якорь под действием силы предварительно поджатой пружины (установлено предварительное поджатие – 2 Н) перемещается в сторону увеличения зазора до упора х = 3 мм. В момент времени 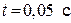 включается источник питания и якорь под действием электромагнитной силы перемещается в сторону уменьшения зазора до упора х =1 мм. При
включается источник питания и якорь под действием электромагнитной силы перемещается в сторону уменьшения зазора до упора х =1 мм. При 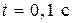 источник питания выключается и якорь возвращается в положение х =3 мм. В момент времени
источник питания выключается и якорь возвращается в положение х =3 мм. В момент времени 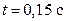 снова включается источник питания и якорь перемещается в положение х =1 мм. В период переходного процесса включения источника питания изменение тока имеет характерный всплеск из-за перемещения якоря.
снова включается источник питания и якорь перемещается в положение х =1 мм. В период переходного процесса включения источника питания изменение тока имеет характерный всплеск из-за перемещения якоря.
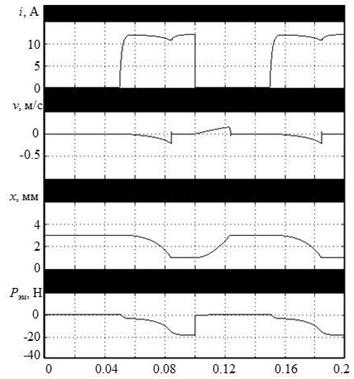
Рис. 1.77. Временные зависимости тока, скорости, перемещения якоря и электромагнитной
На рис. 1.98 изображен разрез высоковольтного ввода с встроенным трансформатором тока. Вводы служат для подсоединения выключателя к шинам распределительного устройства. Ввод состоит из литой эпоксидной втулки 8 с контактным стержнем, фарфоровой покрышки 7 и помещенных в колпак 9 трансформаторов тока 10. В зоне расположения трансформаторов тока 10 цилиндрическая поверхность эпоксидной втулки 8 имеет металлическое покрытие, на верхней части которого установлен экран 13. Покрытие и экран имеют потенциал земли. Пространство между втулкой 8 и фарфоровой покрышкой 7 заполнено изоляционным материалом 14 и с помощью прокладок 16, 17 и наконечника 4 загерметизировано от окружающей среды. Ввод крепится к баку с помощью болтов 11.
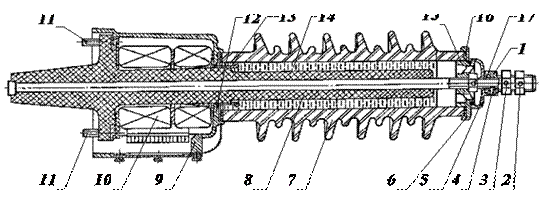
Рис. 1. 98. Конструкция ввода: 1-гайка; 2,3-стопорный винт; 4-наконечник; 5-крышка; 6-фланец; 7-фарфоровая покрышка; 8-литая эпоксидная втулка; 9-колпак; 10-трансформатор тока встроенный; 11-болты; 12,15-уплотнительные кольца; 13-экран; 14-винипол; 16,17- прокладки.
Встроенный трансформатортока состоит из магнитопровода и двух обмоток: защитной и измерительной. Трансформатор тока выполнен в виде тороида (рис. 1.99). Магнитопровод – ленточный из электротехнической стали. Роль первичной обмотки трансформатора тока выполняет контактный стержень ввода. Вторичная обмотка намотана равномерно на магнитопроводе.

Рис. 1. 99. Изготовление трансформатора тока.
Принцип работы трансформатора тока поясним на модели двухобмоточного трансформатора напряжения, схема которого приведена на рис. 1.100.
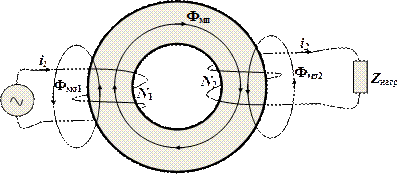
Рис. 1. 100. Схема двухобмоточного трансформатора напряжения: U - напряжение питания первичной обмотки; N 1, N 2 - числа витков первичной и вторичной обмоток; Z нагр - комплексное сопротивление нагрузки.
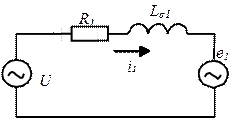
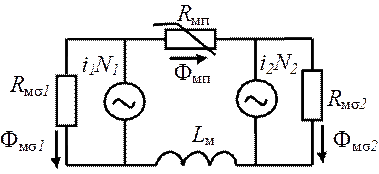
Эквивалентные схемы электрических подсистем первичной и вторичной обмоток трансформатора показаны на рис. 1.101, а,б и магнитной цепи на рис. 1.101, с. Выделены магнитные потоки рассеяния обмоток и рабочий магнитный поток.
 а) а) | 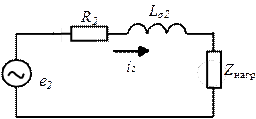 б) б) |
 в) в) |
Рис. 1.101. Эквивалентные схемы двухобмоточного трансформатора: а - первичная электрическая обмотки; б - вторичная электрическая цепь; в - магнитная цепь.
На схемах обозначено:
¾ в первичной обмотке: 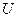 - напряжение питания,
- напряжение питания, 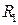 - сопротивление провода,
- сопротивление провода, 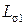 - индуктивность магнитных потоков рассеяния,
- индуктивность магнитных потоков рассеяния, 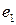 - индуцируемая ЭДС рабочим магнитным потоком;
- индуцируемая ЭДС рабочим магнитным потоком;
¾ во вторичной обмотке: 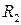 - сопротивление провода,
- сопротивление провода, 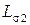 - индуктивность магнитных потоков рассеяния,
- индуктивность магнитных потоков рассеяния, 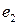 - индуцируемая ЭДС рабочим магнитным потоком,
- индуцируемая ЭДС рабочим магнитным потоком, 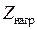 - комплексное сопротивление нагрузки трансформатора;
- комплексное сопротивление нагрузки трансформатора;
¾ в магнитной цепи: 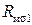 ,
, 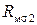 - магнитные сопротивления рассеяния первичной и вторичной обмотки,
- магнитные сопротивления рассеяния первичной и вторичной обмотки, 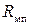 - нелинейное магнитное сопротивление сердечника,
- нелинейное магнитное сопротивление сердечника, 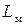 - магнитная индуктивность, определяющая активные потери в сердечнике от индуцируемых токов и магнитного гистерезиса (см. раздел 1.4.3),
- магнитная индуктивность, определяющая активные потери в сердечнике от индуцируемых токов и магнитного гистерезиса (см. раздел 1.4.3), 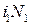 ,
, 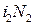 - магнитодвижущие силы первичной и вторичной обмоток;
- магнитодвижущие силы первичной и вторичной обмоток; 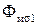 ,
, 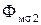 - магнитные потоки рассеяния первичной и вторичной обмоток,
- магнитные потоки рассеяния первичной и вторичной обмоток, 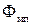 - рабочий магнитный поток в сердечнике.
- рабочий магнитный поток в сердечнике.
Модель трансформатора, составленная по приведенным эквивалентным схемам в программной среде Matlab Simulink изображена на рис. 1. 102.
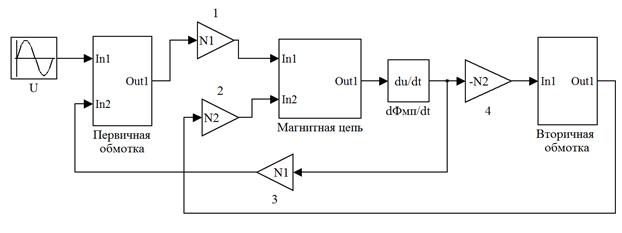
Рис. 1.102. Модель двухобмоточного трансформатора в программной среде Matlab Simulink.
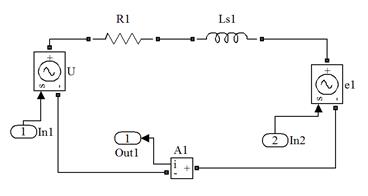
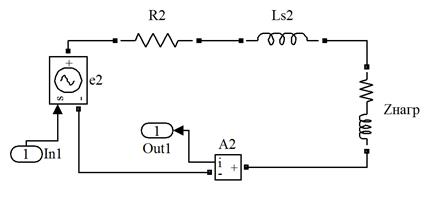
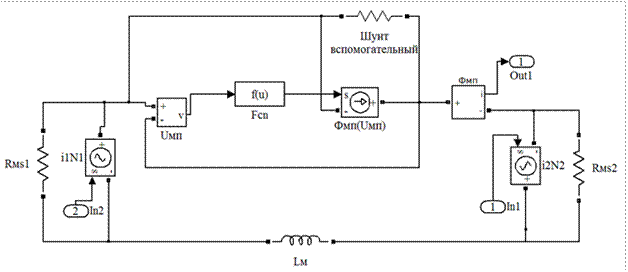
Модель включает три подсистемы: первичной и вторичной обмоток и магнитной цепи трансформатора, которые приведены на рис. 1.103. Подсистемы связаны управляемыми источниками напряжения. Индуцируемые в обмотках ЭДС е1 и е2 получают сигнал управления о рабочем магнитном потоке Фмп из магнитной подсистемы. Этот сигнал дифференцируется и умножается на число витков обмотки. В магнитной подсистеме МДС i 1 N 1 и i 2 N 2. представлены управляемыми источниками напряжения по значениям токов первичной и вторичной обмоток, которые дают амперметры в соответствующих цепях (см. рис. 1.103). Модель нелинейного магнитного сопротивления сердечника трансформатора R мп составлена в виде управляемого источника тока (магнитного потока) Фмп(U мп), который представляет вебер-амперную характеристика сердечника, заданную аппроксимирующей функцией 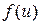 в элементе
в элементе 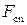 как функция измеряемого вольтметром магнитного напряжения U мп.
как функция измеряемого вольтметром магнитного напряжения U мп.
а)
б)
в)
Рис. 1.103. Эквивалентные схемы подсистем трансформатора в Matlab Simulink: а,б - схемы первичной и вторичной обмоток; в - магнитная цепь.
У трансформатора тока считается заданным ток в первичной обмотке, поэтому нет необходимости включать в расчет первичную обмотку как у трансформатора напряжения и модель будет иметь вид схемы, представленной на рис. 1.104. Здесь источник тока (измеряемый ток) управляет МДС первичной обмотки в магнитной подсистеме.
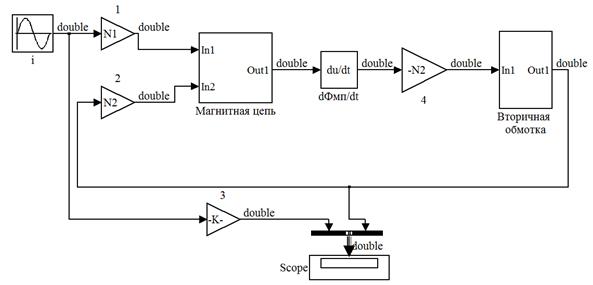
Рис. 1. 104. Модель трансформатора тока в программной среде Matlab Simulink.
Конструкция трансформатора тока, магнитные свойства материала сердечника, значения первичного тока и нагрузки вторичной обмотки влияют на возникающие погрешности измерения тока и его угла. Моделирование процессов позволяет выполнить теоретический анализ возникающих погрешностей. Для примера рассмотрим встроенный трансформатор тока типаТВ-35-III. Габаритный чертеж трансформатора приведен на рис. 1.105, а его технические характеристики в табл. 1.5.
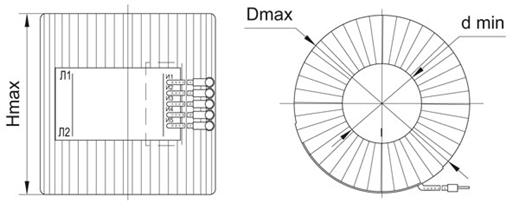
Рис. 1.105. Габаритный чертеж трансформатора тока ТВ-35-III.
Таблица 1.5
Технические характеристики трансформатора тока ТВ-35-III
| Тип трансформатора | Номинальный первичный ток, А | Номиналь-ный вто-ричный ток, А | Размеры, мм | Масса max, кг | Климати-ческое исполнение | ||
| D max | d min | H max | |||||
| ТВ-35-III | 200-1500 | У2 |
| Вариант исполнения | Номинальный ток, А | Вторичная нагрузка при cos φ=0,8 в классе точности, В∙А | Ток термической стойкости, кА (кратность) | Номинальная предельная кратность | Длительность протекания тока КЗ, с | |
| первич-ный | вторич-ный | |||||
| 200/5 |
Результаты моделирования в диапазоне номинальных первичных токов и указанной в табл. 1.5 комплексной нагрузки трансформатора (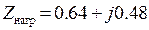 ) показывают на существование токовой и угловой погрешности (см. рис. 1.106) в пределах установленных значений класса точности.
) показывают на существование токовой и угловой погрешности (см. рис. 1.106) в пределах установленных значений класса точности.
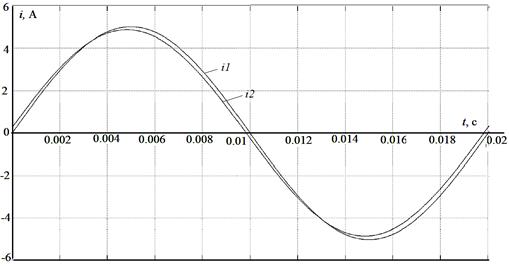
Рис. 1.106. Мгновенные значения токов первичной и вторичной обмоток в номинальном режиме. Ток первичной обмотки приведен ко вторичному.
При превышении номинальной предельной кратности тока погрешности увеличиваются, а при значительном превышении допустимой кратности возникают искажения вторичного тока из-за явления магнитного насыщения материала сердечника.
Ток вторичной обмотки зависит от сопротивления нагрузки трансформатора. Как изменяется соотношение между первичным и вторичным током при возрастании сопротивления нагрузки показывает зависимость на рис. 1.107. Приведенные зависимости подтверждают, что допустимые погрешности измерений тока возможны только при малых значениях сопротивления нагрузки, т.е в режиме близком к короткому замыканию
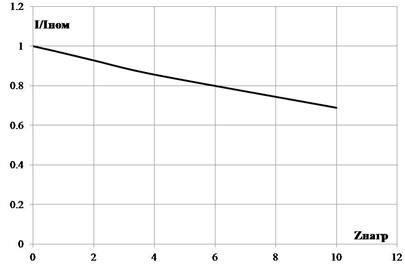
Рис. 1.107. Изменение вторичного тока трансформатора от сопротивления нагрузки (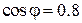 ).
).
 2015-08-21
2015-08-21 4025
4025







