Правило (2) предыдущего параграфа дает нам право определить экспоненту чисто мнимого числа:
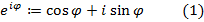
Действительно, таким образом определенная функция 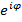 обладает следующими свойствами:
обладает следующими свойствами:
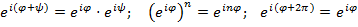
Здесь первое равенство есть частный случай (2) предыдущего параграфа, когда 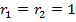 , второе равенство есть не что иное как формула Муавра, а третье равенство вытекает из периодичности гармоник. Заметим, что никакой коллизии в обозначения в связи с известной экспонентой
, второе равенство есть не что иное как формула Муавра, а третье равенство вытекает из периодичности гармоник. Заметим, что никакой коллизии в обозначения в связи с известной экспонентой 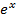 действительной переменной не возникает; равенство аргументов
действительной переменной не возникает; равенство аргументов 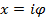 возможно лишь если
возможно лишь если 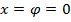 . Но тогда определение (1) комплексной экспоненты дает нам значение
. Но тогда определение (1) комплексной экспоненты дает нам значение 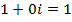 , что совпадает с известным равенством
, что совпадает с известным равенством 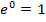 .
.
Определение (1) позволяет записать ненулевое комплексное число в показательной форме
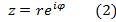
В таком виде легче оперировать с комплексными числами, когда речь идет об умножении, делении и возведении в степень. Например,
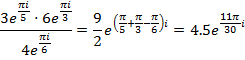
 2015-08-13
2015-08-13 2975
2975








