Изобразим комплексное число 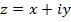 вектором. Длина этого вектора, т.е. величина
вектором. Длина этого вектора, т.е. величина 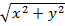 называется модулем комплексного числа
называется модулем комплексного числа 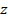 и обозначается
и обозначается 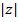 . Если
. Если 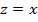 -- действительное число, то приходим к «школьному» модулю, ибо
-- действительное число, то приходим к «школьному» модулю, ибо 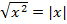 . Если
. Если 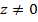 , то угол, который образует вектор
, то угол, который образует вектор 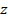 с действительной осью называется аргументом комплексного числа
с действительной осью называется аргументом комплексного числа 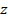 и обозначается
и обозначается 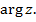 Пусть
Пусть 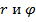 – модуль и аргумент ненулевого комплексного числа. Тогда
– модуль и аргумент ненулевого комплексного числа. Тогда
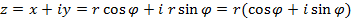 (1)
(1)
Выражение 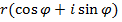 называется тригонометрической формой записи комплексного числа.
называется тригонометрической формой записи комплексного числа.
Свойства модуля. Для любых комплексных чисел 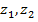 имеют место соотношения:
имеют место соотношения:
а) 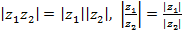 ,
,
б) 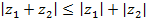 (неравенство треугольника);
(неравенство треугольника);
Докажем первое равенство:
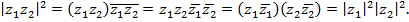
Извлекая квадратный корень, получим равенство 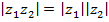 . Второе равенство следует из первого, ибо оно эквивалентно следующему соотношению:
. Второе равенство следует из первого, ибо оно эквивалентно следующему соотношению: 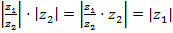 .
.
Докажем неравенство треугольника. Обозначая 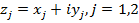 и возводя в квадрат, заменяем это неравенство на равносильное:
и возводя в квадрат, заменяем это неравенство на равносильное:
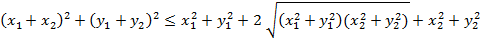
Возводя в квадрат в левой части и сокращая, получаем эквивалентное неравенство
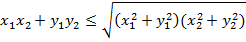
Это неравенство будет следовать из неравенства
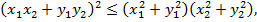
которое, после возведения в квадрат и сокращения, превращается в неравенство
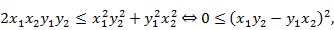
Последнее неравенство несомненно верно. □
Следствие. Множество комплексных чисел с единичным модулем (обозначим: 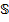 – комплексная единичная окружность) замкнуто относительно умножения и обращения.
– комплексная единичная окружность) замкнуто относительно умножения и обращения.
Перемножим два комплексных числа в тригонометрической форме записи:
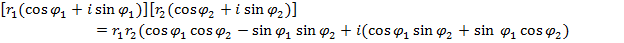
Применяя тригонометрические формулы «косинус суммы» и «синус суммы», приходим к следующему правилу: при перемножении комплексных чисел модули умножаются, а аргументы складываются
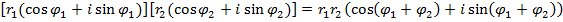 (2)
(2)
В частности, перемножая число 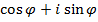 на себя n раз, получаем формулу Муавра:
на себя n раз, получаем формулу Муавра:
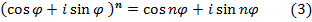
Умножая произвольное комплексное число-вектор 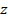 на комплексное число вида
на комплексное число вида 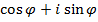 , увеличиваем аргумент у комплексного числа
, увеличиваем аргумент у комплексного числа 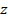 на величину
на величину 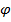 , не меняя модуля. Это преобразование соответствует повороту комплексной плоскости на угол
, не меняя модуля. Это преобразование соответствует повороту комплексной плоскости на угол 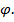 Умножение на положительное действительное число
Умножение на положительное действительное число 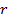 есть гомотетия комплексной плоскости (растяжение в
есть гомотетия комплексной плоскости (растяжение в 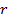 раз, если
раз, если 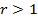 и сжатие в
и сжатие в  раз, если
раз, если 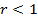 ). Итак, преобразование
). Итак, преобразование
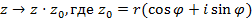
представляет из себя последовательное выполнение двух геометрических преобразований над вектором 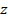 -- поворота и гомотетии. В этом и заключается геометрический смысл умножения комплексных чисел.
-- поворота и гомотетии. В этом и заключается геометрический смысл умножения комплексных чисел.
Пример. Вычислим 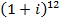 . Для этого сначала найдем модуль и аргумент числа
. Для этого сначала найдем модуль и аргумент числа 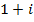 :
:
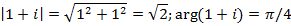
Для того чтобы найти аргумент изобразим комплексное число 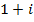 вектором, очевидно лежащем на биссектрисе первого квадранта, и ответ
вектором, очевидно лежащем на биссектрисе первого квадранта, и ответ 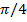 или, по другому,
или, по другому, 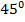 станет понятен. Далее
станет понятен. Далее
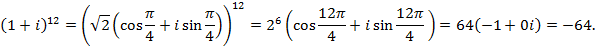
 2015-08-13
2015-08-13 1442
1442
