Многочлен с переменной 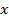 имеет вид
имеет вид
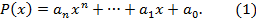
Величины 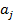 -ые, суть коэффициенты многочлена, могут быть целыми или рациональными или действительными или комплексными. Мы рассматриваем многочлены как функции одного переменного, если переменной
-ые, суть коэффициенты многочлена, могут быть целыми или рациональными или действительными или комплексными. Мы рассматриваем многочлены как функции одного переменного, если переменной 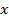 придано значение
придано значение 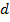 , то значение многочлена
, то значение многочлена 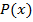 в этой точке равно
в этой точке равно 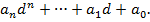 Если
Если 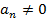 , то коэффициент
, то коэффициент 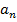 называется старшим; в этом случае говорят, что многочлен
называется старшим; в этом случае говорят, что многочлен 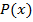 имеет степень
имеет степень 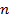 (записываем как
(записываем как 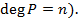 В частности,
В частности, 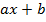 есть общий вид линейного многочлена, а
есть общий вид линейного многочлена, а 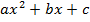 есть общий вид квадратного трехчлена (
есть общий вид квадратного трехчлена (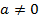 ). Удобно считать, что степень нулевого многочлена есть
). Удобно считать, что степень нулевого многочлена есть 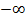 , и эта величина меньше чем любая другая возможная степень –
, и эта величина меньше чем любая другая возможная степень – 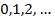 Многочлены, как и всякие функции, можно складывать и умножать. Пусть
Многочлены, как и всякие функции, можно складывать и умножать. Пусть 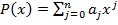 ,
, 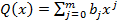 . Тогда
. Тогда
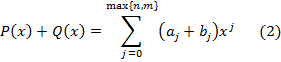
Здесь и далее полагаем, что если многочлен задан соотношением (1), то 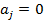 при всех
при всех 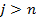 . Таким образом
. Таким образом
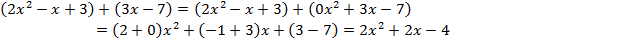
Умножаются многочлены путем стандартной процедуры раскрытия скобок и приведения подобных слагаемых. Это приводит к следующему правил умножения многочленов
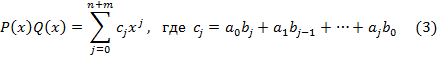
Отметим, что сумма и разность многочленов, а также произведение многочленов есть многочлены.
Отметим свойства степени многочлена
А. 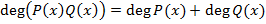 . Заметим, что это свойство верно и в том случае, когда один или оба из многочленов
. Заметим, что это свойство верно и в том случае, когда один или оба из многочленов 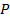 и
и 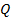 нулевые. Для этого надо считать, что
нулевые. Для этого надо считать, что 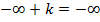 для любого элемента
для любого элемента 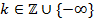 .
.
Б. 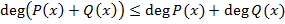 . Если степени многочленов
. Если степени многочленов 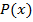 и
и 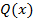 различны, то здесь имеет место равенство.
различны, то здесь имеет место равенство.
Деление многочленов с остатком. Для любых многочленов 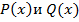 таких, что
таких, что 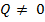 найдется многочлен
найдется многочлен 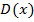 -- неполное частное и
-- неполное частное и 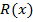 – остаток, для которых верно равенство
– остаток, для которых верно равенство 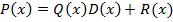 , причем степень остатка меньше чем степень делителя
, причем степень остатка меньше чем степень делителя 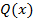 .
.
Обоснуем метод деления с остатком, применяя индукцию по степени делимого. База индукции, случай 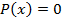 . Тогда надо взять
. Тогда надо взять 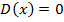 и
и 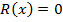 . Пусть для
. Пусть для 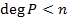 метод обоснован, и сейчас
метод обоснован, и сейчас 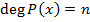 . Тогда
. Тогда 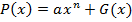 , где
, где 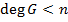 . Обозначим через
. Обозначим через 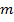 степень делителя. Тогда
степень делителя. Тогда 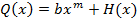 где
где 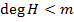 . По определению
. По определению 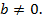 Можно считать
Можно считать 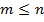 , ибо иначе следует положить
, ибо иначе следует положить 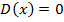 и
и 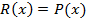 . Рассмотрим разность
. Рассмотрим разность
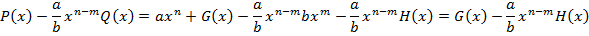
Этот многочлен имеет степень меньшую чем 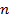 (см. свойство степеней Б), следовательно, найдутся
(см. свойство степеней Б), следовательно, найдутся 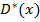 -- неполное частное и
-- неполное частное и 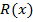 – остаток, такие, что
– остаток, такие, что
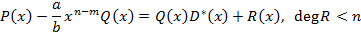
Искомый остаток есть 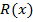 , а искомое неполное частное
, а искомое неполное частное 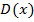 есть
есть 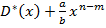
Пример. Разделим 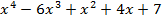 на
на 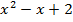 c остатком «уголком»:
c остатком «уголком»:
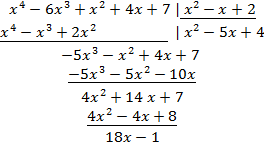
Итак, 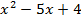 -- неполное частное, а
-- неполное частное, а 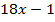 -- остаток. Имеет место равенство
-- остаток. Имеет место равенство
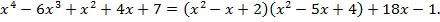
Определение. Число 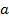 есть корень многочлена
есть корень многочлена 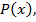 если
если 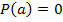 .
.
Теорема Безу. Число 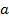 есть корень многочлена
есть корень многочлена 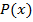 тогда и только тогда, когда
тогда и только тогда, когда 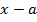 делит
делит 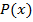 нацело, без остатка.
нацело, без остатка.
Доказательство. Поделим 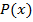 на
на 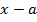 с остатком:
с остатком:
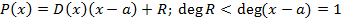
Так как 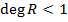 , то
, то 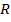 -- константный многочлен. Тогда
-- константный многочлен. Тогда 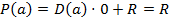 . Следовательно, число
. Следовательно, число 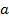 – корень многочлена
– корень многочлена 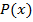 в том и только том случае, когда
в том и только том случае, когда 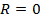 , а это имеет место ровно тогда, когда
, а это имеет место ровно тогда, когда 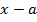 делит
делит 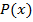 .□
.□
Пусть 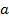 -- корень многочлена
-- корень многочлена 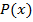 . Тогда
. Тогда 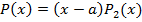 по теореме Безу. Если
по теореме Безу. Если 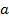 -- корень многочлена
-- корень многочлена 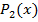 , то мы можем и от него отщепить
, то мы можем и от него отщепить 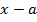 . Будем это делать до тех пор пока
. Будем это делать до тех пор пока 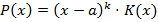 и
и 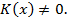 В этом случае
В этом случае 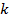 называют кратностью корня
называют кратностью корня 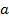 . Итак, кратностью корня
. Итак, кратностью корня 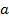 многочлена
многочлена 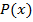 называется наибольшее натуральное число
называется наибольшее натуральное число 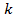 такое, что
такое, что 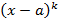 делит
делит 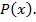 Если
Если 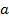 не является корнем многочлена
не является корнем многочлена 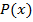 , то удобно считать, что кратность
, то удобно считать, что кратность 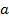 есть 0.
есть 0.
Предложение. Число 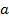 имеет кратность k в том и только том случае, когда
имеет кратность k в том и только том случае, когда 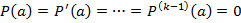 и
и 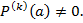
Доказательство. Пусть 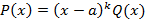 и
и 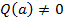 . Тогда
. Тогда
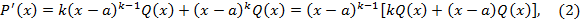
при этом значение многочлена 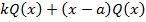 в точке
в точке 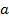 не равно нулю. Это дает возможность применить индукцию по
не равно нулю. Это дает возможность применить индукцию по 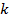 и заключить, что все производные от
и заключить, что все производные от 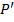 порядка
порядка 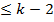 равны 0, а производная порядка
равны 0, а производная порядка 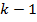 не равна 0. Тогда
не равна 0. Тогда 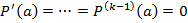 и
и 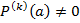 . База индукции, случай
. База индукции, случай 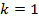 также следует из (2).
также следует из (2).
Наоборот, пусть выполнены соотношения 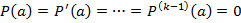 и
и 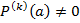 .. Применим формулу Тейлора к многочлену
.. Применим формулу Тейлора к многочлену 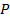 в точке
в точке 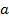 , считая
, считая 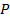 многочленом степени
многочленом степени 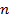 :
:
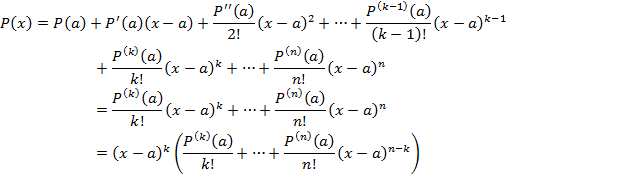
При этом многочлен 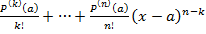 в точке
в точке 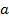 равен
равен 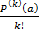 и тем самым не равен 0.□
и тем самым не равен 0.□
 2015-08-13
2015-08-13 2170
2170








