Алгебраической причиной введения комплексных чисел является отсутствие действительного корня уравнения 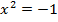 . В самом деле,
. В самом деле, 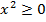 для любого действительного
для любого действительного 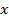 , причем
, причем 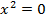 лишь если
лишь если 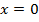 . Но именно это обстоятельство позволяет расширить область действительных чисел
. Но именно это обстоятельство позволяет расширить область действительных чисел 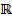 до поля комплексных чисел
до поля комплексных чисел 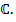
Комплексное число имеет вид 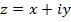 , где
, где 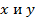 -- вещественные числа, называемые действительной и мнимой частью комплексного числа z (записываем так:
-- вещественные числа, называемые действительной и мнимой частью комплексного числа z (записываем так: 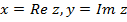 ), а
), а 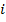 -- новое число, называемое комплексной единицей и обладающее свойством
-- новое число, называемое комплексной единицей и обладающее свойством 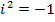 . Два комплексных числа равны в том и только том случае, когда совпадают их действительные и мнимые части. Операции сложения и умножения над комплексными числами определяются следующим образом
. Два комплексных числа равны в том и только том случае, когда совпадают их действительные и мнимые части. Операции сложения и умножения над комплексными числами определяются следующим образом
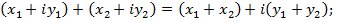
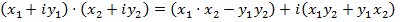 (1)
(1)
Нулевое комплексное число 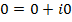 нейтрально по отношению к сложению (т.е.
нейтрально по отношению к сложению (т.е. 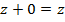 для всех
для всех 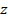 ), а единица
), а единица 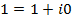 нейтрально по отношению к умножению. Противоположное комплексное число
нейтрально по отношению к умножению. Противоположное комплексное число 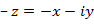 обладает тем свойством, что
обладает тем свойством, что 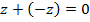 . Прямым способом проверяются свойства ассоциативности и коммутативности сложения и умножения, а также дистрибутивность умножения относительно сложения:
. Прямым способом проверяются свойства ассоциативности и коммутативности сложения и умножения, а также дистрибутивность умножения относительно сложения:
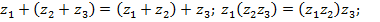
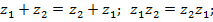
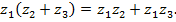
Заметим, что равенство 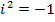 следует из определения (1), а именно
следует из определения (1), а именно
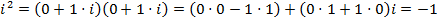 .
.
Здесь и далее мы отождествляем комплексное число 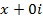 с действительным числом
с действительным числом 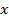 . Возможность такого отождествления обосновывается тем, что
. Возможность такого отождествления обосновывается тем, что
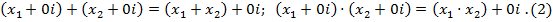
Заметим, что в этих равенствах знаки сложения и умножения использованы в двух смыслах: как сложение (умножение) действительных чисел 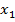 и
и 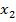 и как сложение (умножение) двух комплексных числе
и как сложение (умножение) двух комплексных числе 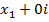 и
и 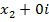 согласно определению (1).
согласно определению (1).
Если 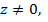 то либо
то либо 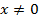 , либо
, либо 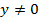 , и поэтому
, и поэтому 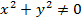 . В этом случае комплексное число
. В этом случае комплексное число 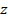 имеет обратное
имеет обратное
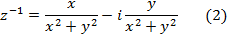
Действительно,
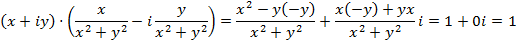
Тем самым совокупность всех комплексных чисел 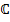 превращается в поле. Поле действительных чисел изоморфно вкладывается в поле
превращается в поле. Поле действительных чисел изоморфно вкладывается в поле 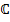 посредством отображения
посредством отображения 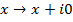 , как это уже было отмечено в равенствах (2).
, как это уже было отмечено в равенствах (2).
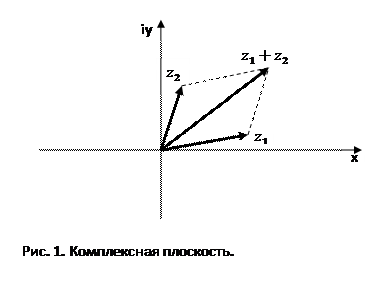 Комплексные числа изображаются точками на плоскости Oxy или векторами с начальной точкой в начале координат (см. рис. 1). Горизонтальная ось Ox называется действительной осью, а вертикальная ось Oy называется мнимой осью и обозначается как
Комплексные числа изображаются точками на плоскости Oxy или векторами с начальной точкой в начале координат (см. рис. 1). Горизонтальная ось Ox называется действительной осью, а вертикальная ось Oy называется мнимой осью и обозначается как 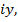 ибо по ней откладываются чисто мнимые числа
ибо по ней откладываются чисто мнимые числа 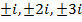 и.т.д.. При этом сложение двух комплексных чисел можно рассматривать как сложение двух векторов по правилу параллелограмма. Геометрическая интерпретация умножения будет указана позже.
и.т.д.. При этом сложение двух комплексных чисел можно рассматривать как сложение двух векторов по правилу параллелограмма. Геометрическая интерпретация умножения будет указана позже.
Примеры. А. 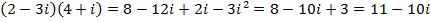
Б. 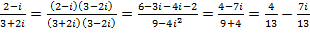
В.  . В частности
. В частности 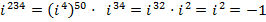 .
.
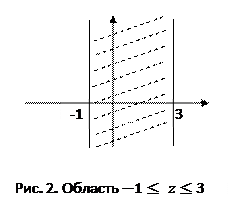 Г. Нарисуем область комплексных чисел
Г. Нарисуем область комплексных чисел 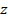 , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 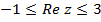 . Ответ см. на рис. 2.
. Ответ см. на рис. 2.
 2015-08-13
2015-08-13 2140
2140