Решение квадратных уравнений

Линейный многочлен 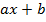всегда имеет корень 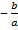. Квадратный трехчлен уже не всегда имеет корни.

Пусть 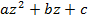– квадратный трехчлен над полем комплексных чисел (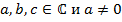). Обозначим через 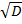какой-либо комплексный квадратный корень из дискриминанта 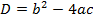. Тогда

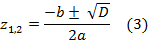
суть комплексные корни многочлена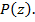

Действительно, уравнение 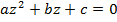равносильно уравнению 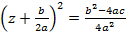, откуда и следует формула (3).

Пример. Решим уравнение :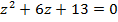

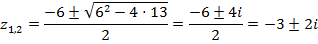
Заметим, что как и положено по теореме Виета, сумма корней равна 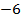, а произведение равно 13.