C помощью комплексной экспоненты легко извлекаются корни из комплексных чисел. Решим уравнение 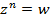 . Если w=0, то имеется только один нулевой корень кратности n. Пусть
. Если w=0, то имеется только один нулевой корень кратности n. Пусть 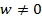 . Запишем
. Запишем 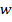 в показательном виде
в показательном виде 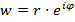 , где
, где 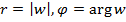 . Найдем арифметический корень n-ой степени из r и обозначим его
. Найдем арифметический корень n-ой степени из r и обозначим его 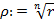 . Тогда уравнение
. Тогда уравнение 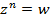 имеет n корней, расположенных на окружности радиуса
имеет n корней, расположенных на окружности радиуса 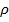 в вершинах правильного n-угольника
в вершинах правильного n-угольника
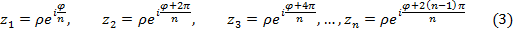
/*/ Действительно, применяя формулу Муавра, легко проверить, что все 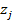 -- корни уравнения
-- корни уравнения 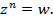 Пусть
Пусть 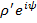 – какой-либо корень уравнения
– какой-либо корень уравнения 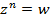 . Тогда
. Тогда 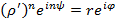 . Приравнивая модули, получаем равенство
. Приравнивая модули, получаем равенство 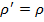 . Сокращая на
. Сокращая на 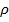 и деля на
и деля на 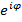 , получим
, получим 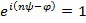 откуда
откуда 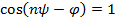 и
и 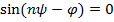 . Это значит, что
. Это значит, что 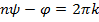 для некоторго целого
для некоторго целого 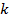 . Поделим
. Поделим 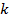 на
на 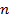 с остатком:
с остатком: 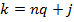 , где
, где 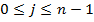 . Тогда
. Тогда
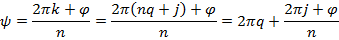
и 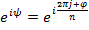 . Следовательно,
. Следовательно, 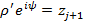 .
.
Корни (3) расположены в вершинах правильного 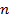 - угольника, вписанного в окружность радиуса
- угольника, вписанного в окружность радиуса 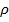 , имеющей центр в нулевой точке.
, имеющей центр в нулевой точке.
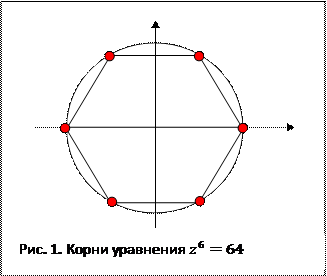 Например, найдем корни уравнения
Например, найдем корни уравнения 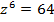 . Здесь
. Здесь 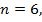 арифметический корень шестой степени из 64 равен 2, а агрумент
арифметический корень шестой степени из 64 равен 2, а агрумент 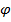 равен нулю. Следовательно, корни имеют вид
равен нулю. Следовательно, корни имеют вид
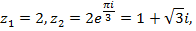
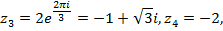
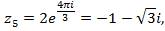
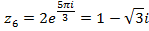
 2015-08-13
2015-08-13 1362
1362








