Основная теорема алгебры комплексных чисел

Решив казалось бы частную задачу о поле комплексных чисел, в котором уравнение 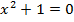имеет корень, мы одновременно справились со всеми остальными полиномиальными уравнениями.

Основная теорема алгебры. Любой многочлен над полем комплексных чисел, не равный константе, имеет хотя бы один комплексный корень.

Следствие. Любой многочлен, не равный константе, над полем комплексных чисел разложим в произведение линейных множителей.

Доказательство следствия представляет из себя несложную индукцию по степени многочлена.

Над полем действительных чисел существуют по крайней мере два вида неприводимых многочленов: -- линейные и квадратичные c отрицательным дискриминантом. Оказывается, что эти два случая исчерпывают множество неприводимых многочленов над ℝ.

Теорема. Любой многочлен над полем действительных чисел разложим в произведение линейных множителей и квадратичных множителей с отрицательными дискриминантами.

В начале докажем лемму 5: Есл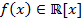и и 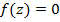для какого-либо 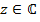, то сопряженное число 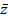также является корнем многочлена .

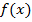Доказательство. Пусть 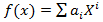, 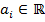и 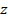– комплексный корень многочлена 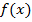. Тогда

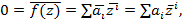
где мы использовали свойства сопряжения. Следовательно, 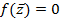. Тем самым 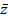-- корень многочлена . □

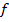Доказательство теоремы. Достаточно доказать, что любой неприводимый многочлен над полем действительных чисел либо линейный, либо квадратичный с отрицательным дискриминантом. Пусть 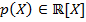-- неприводимый многочлен с единичным старшим коэффициентом. В случае 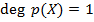сразу получаем 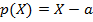для некоторого действительного 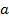. Предположим, что 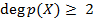. Обозначим через 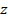какой-либо комплексный корень этого многочлена, существующий по основной теореме алгебры комплексных чисел. Так как 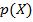неприводим, то 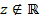(см. теорему Безу). Тогда по лемме 5, 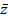будет еще одним корнем многочлена 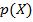, отличным от .

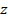Многочлен 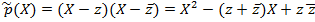имеет действительные коэффициенты т.к. 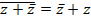и 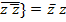. Кроме того, 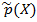делит 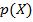согласно теореме Безу. Так как 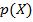неприводим и имеет единичный старший коэффициент, то получаем равенство 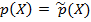. Дискриминант этого многочлена отрицателен, так как иначе он имел бы вещественные корни.□