Для любых векторов x и y евклидова пространства E со скалярным призведением (x, y) справедливо неравенство:
|(x, y)|2 ≤ (x, x)·(y, y).
Нормированное линейное пр-во
Угол между двумя эл-ми в евклидовом пр-ве
Углом между двумя произвольными векторами х,у евклидова пространства называется угол
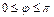 , косинус которого вычисленное по формуле
, косинус которого вычисленное по формуле 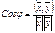
Ортогональность эл-тов в евклидовом пр-ве
Два любых эл-та х и у евклидова пр-ва называются ортогональными, если скалярное произведение этих эл-тов =0 (Cosφ=0). Назовем сумму 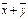 двух ортогональных эл-тов
двух ортогональных эл-тов 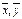 гипотенузой прямоугольного треугольника, построенного на эл-тах х,у.В любом евклидовом пр-ве справедлива теорема Пифагора
гипотенузой прямоугольного треугольника, построенного на эл-тах х,у.В любом евклидовом пр-ве справедлива теорема Пифагора 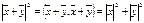
 2015-08-13
2015-08-13 390
390








