Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
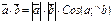
Св-ва:1. 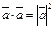
2. 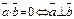 или один из векторов =
или один из векторов = 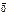
3. 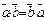
4. 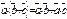
5. 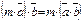 ,m- число
,m- число
Векторное произведение векторов
Векторным произведением векторов a и b называется вектор с, который удовлетворяет следующие условия:
1. 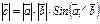
2. 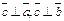
3.Векторы a,b,c образуют правую тройку
Св-ва: 1. 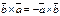
2. 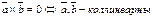
3. 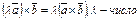
4. 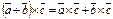
Смешанное произведение векторов
Смешанным произведением трех векторов a,b,c называется число, равное векторному произведению 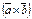 , умноженному скалярно на вектор c.
, умноженному скалярно на вектор c. 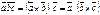
Св-ва: 1. 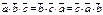
2. 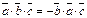
3. 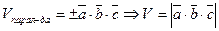
4. 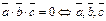 - компланарны (принадлежат одной пл-ти)
- компланарны (принадлежат одной пл-ти)
Собственные значения и собственные векторы линейного оператора
Определение: число λ называется собственным значением линейного оператора А, если существует не 0 вектор х такой, что 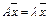
Утверждение: для того, чтобы число λ было собственным значением линейного оператора А необходимо и достаточно, чтобы это число было корнем характеристического уравнения:
det(A-λE)=0
Св-ва: 1.Все собственные векторы принадлежат одному и тому же собственному значению, вместе с нулевым вектором образуют линейное подпространство.
2.Если собств.векторы принадлежат попарно различным собств.значениям, то они линейно -независимы.
3.Пусть собств.значение λ лин.преобраз.А является корнем характеристического ур-ия кратности с, тогда ему принадлежит не более с линейно-независимо собств.векторов.
Определение вещественного евклидова пр-ва:
Линейное пр-во L называется евклидовым пр-вом, если: 1.есть правило по которому любым 2-ум эл-там 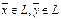 ставится в соответствии действ.число называемое скалярным произведением этих эл-тов и обозначаемое
ставится в соответствии действ.число называемое скалярным произведением этих эл-тов и обозначаемое 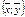
2.Это правило подчинено след.аксиомам
I. 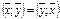 II.
II. 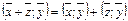
III. 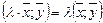
IV. 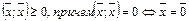
 2015-08-13
2015-08-13 388
388







