Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.
· Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, 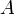 (м)
(м)
· Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), 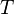 (с)
(с)
· Частота — число колебаний в единицу времени, 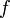 (Гц, с−1).
(Гц, с−1).
Период колебаний 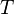 и частота
и частота 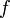 — обратные величины;
— обратные величины;
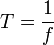 и
и 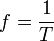
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота 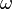 (рад/с, Гц, с−1), показывающая число колебаний за
(рад/с, Гц, с−1), показывающая число колебаний за 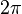 единиц времени:
единиц времени:
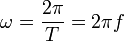
· Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр.
· Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания
По лекции: из правила Кирхгофа имеем: 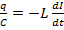
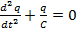 ;
; 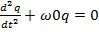 ;
; 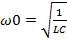 ;
; 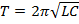 ;
;
q=q0 cos(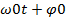 ); I=
); I= 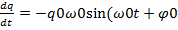 )
)
U= 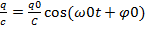 .
.
Не из лекции:
Резонансная частота контура определяется так называемой формулой Томсона:
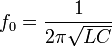
Процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности.
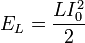 , где
, где 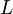 — индуктивность катушки,
— индуктивность катушки, 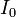 — максимальное значение тока.
— максимальное значение тока.
Напряжение, возникающее в катушке при изменении протекающего тока равно
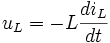
Аналогично для тока, вызванного изменением напряжения на конденсаторе:
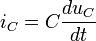
Поскольку всё возникающее в катушке напряжение падает на конденсаторе, то 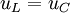 , а ток, вызванный конденсатором проходит через катушку, то
, а ток, вызванный конденсатором проходит через катушку, то 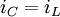 . Дифференцируя одно из уравнений и подставляя результат в другое, получаем
. Дифференцируя одно из уравнений и подставляя результат в другое, получаем
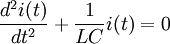
Это уравнение гармонического осциллятора с циклической частотой 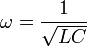
Решением такого уравнения является
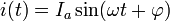
где 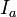 — некая постоянная, называемая амплитудой колебаний,
— некая постоянная, называемая амплитудой колебаний, 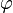 — также некоторая постоянная, называемая начальной фазой. И, например, при начальных условиях
— также некоторая постоянная, называемая начальной фазой. И, например, при начальных условиях 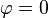 решение сведётся к
решение сведётся к
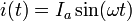
Решение может быть записано также в виде
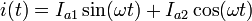
где 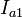 и
и 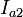 — некоторые константы, которые связаны с амплитудой
— некоторые константы, которые связаны с амплитудой 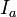 и фазой
и фазой 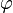 следующими отношениями
следующими отношениями
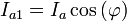
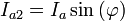
 2015-08-13
2015-08-13 2115
2115
