Затухающие колебания — колебания, энергия которых уменьшается с течением времени.
Затухающие свободные колебания физической величины s описываются дифференциальным уравнением вида: 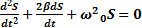 . Постоянная величина β называется коэффициентом затухания. Круговая частота ω0 характеризует свободные колебания той же колебательной системы без затухания и называется частотой собственных колебаний системы.
. Постоянная величина β называется коэффициентом затухания. Круговая частота ω0 характеризует свободные колебания той же колебательной системы без затухания и называется частотой собственных колебаний системы.
S(t)= 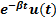 , где u (t) – неизвестная вещественная функция. Тогда исходное дифференциальное уравнение преобразуется в уравнение вида
, где u (t) – неизвестная вещественная функция. Тогда исходное дифференциальное уравнение преобразуется в уравнение вида
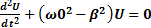 . В зависимости от начальных условий полученное уравнение имеет решение вида U=
. В зависимости от начальных условий полученное уравнение имеет решение вида U= 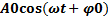
Тогда затухающие колебания величины s описываются функциональными зависимостями типа: S= 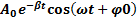 . Неотрицательная величина A 0 является начальной амплитудой затухающих колебаний, величина ϕ0 – начальной фазой этих колебаний. Частота ω, которая называется частотой затухающих колебаний, всегда меньше частоты собственных колебаний ω0. Функция
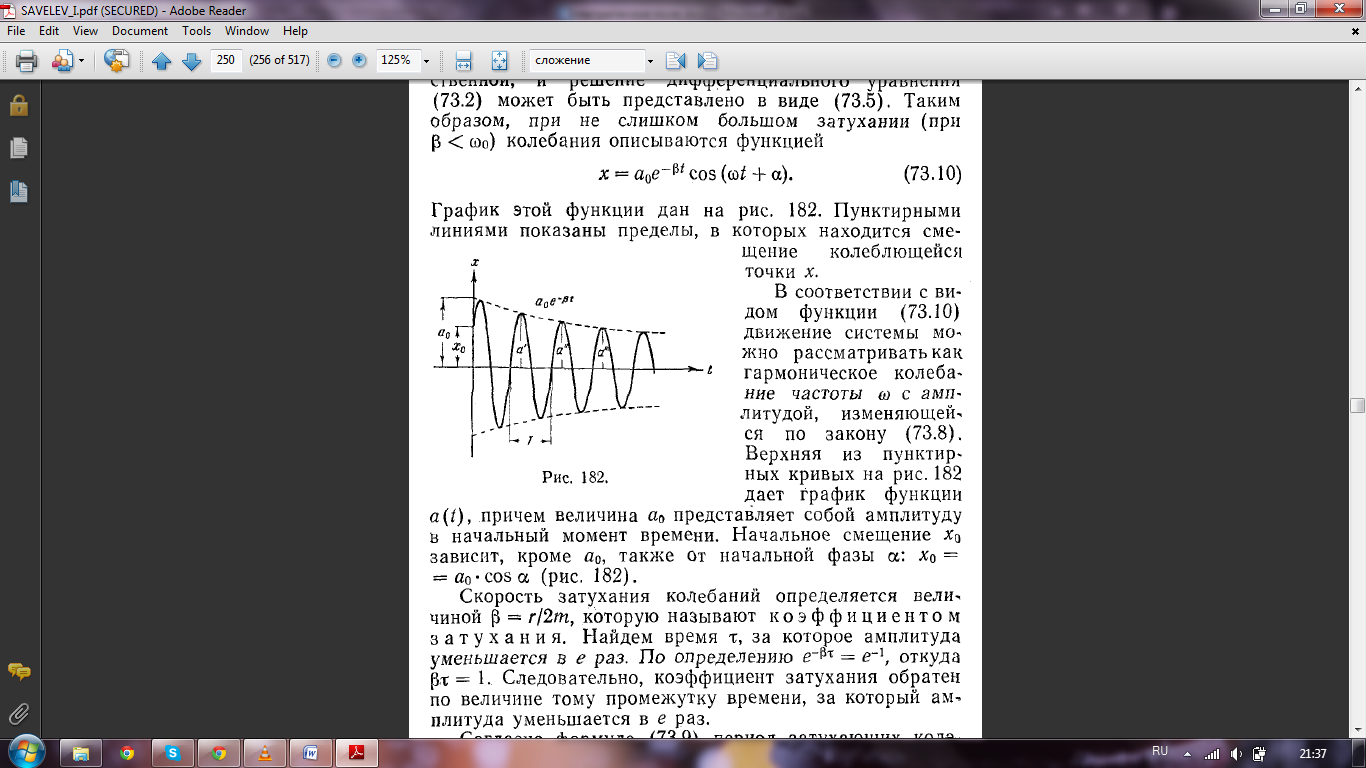
. Неотрицательная величина A 0 является начальной амплитудой затухающих колебаний, величина ϕ0 – начальной фазой этих колебаний. Частота ω, которая называется частотой затухающих колебаний, всегда меньше частоты собственных колебаний ω0. Функция 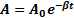 описывает изменение амплитуды свободных колебаний со временем и называется амплитудой затухающих колебаний. Амплитуда затухающих колебаний убы-вает со временем по экспоненциальному закону (рис).
описывает изменение амплитуды свободных колебаний со временем и называется амплитудой затухающих колебаний. Амплитуда затухающих колебаний убы-вает со временем по экспоненциальному закону (рис).
Период затухающих колебаний равен
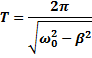
Для количественной характеристики скорости убывания амплитуды затухающих колебаний вводят понятие декремента затухания. Декрементом затухания называется отношение амплитуды затухающих колебаний в некоторый момент времени t к амплитуде тех же колебаний на период позже t + T: 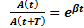
Натуральный логарифм декремента затухания называется логарифмическим декрементом затухания: 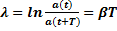 .
.
Для характеристики колебательной системы часто употребляется также величина 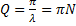 , называемая добротностью колебательной системы.
, называемая добротностью колебательной системы.
Из соотношения 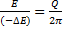 следует, что с ростом коэффициента затухания период колебаний увеличивается. При
следует, что с ростом коэффициента затухания период колебаний увеличивается. При 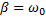 период колебаний обращается в бесконечность, т.е. движение перестает быть периодическим. При
период колебаний обращается в бесконечность, т.е. движение перестает быть периодическим. При 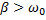 корни характеристического уравнения становятся вещественными и решение дифференциального уравнения оказывается равным сумме двух экспонент:
корни характеристического уравнения становятся вещественными и решение дифференциального уравнения оказывается равным сумме двух экспонент:
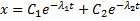
 2015-08-13
2015-08-13 4414
4414
