Тест серий (runs test)

Если мы тщательно рассмотрим Рис. 9, мы заметим следующее: На начальной стадии, мы имеем несколько отрицательных остатков, затем идет серия положительных остатков, а потом снова несколько отрицательных. Если эти остатки совершенно случайны, то можем ли мы наблюдать такую картину? Интуитивно, кажется, что маловероятно. Мы можем проверить интуицию с помощью, так называемого теста серий.

Для того, чтобы объяснить тест серий, давайте просто выпишем знаки перед остатками регрессии (доходы — продуктивность), которые даны в третьей и восьмой колонках таблицы 2.

(– – – – – – – – –) (+ + + + + + + + + + + + + + + + + + + + +) (– – – – – – – – – –)

Таким образом, получаем последовательность из 9 отрицательных, 21 положительного и 10 отрицательных остатков, всего 40 наблюдений.

Определим также как серию непрерывную последовательность одного знака, такого как + или –. В дальнейшем также мы будем определять как длину серии (ряда) как количество элементов в нем. В последовательности, показанной на выше, есть три серии: серия из 9 минусов (длина серии 9), серия из 21 плюса (длина серии 21) и серия из 10 минусов (длина серии 10). Для лучшего визуального представления, серии представлены в скобках.

Рассматривая, как серии ведут себя в абсолютно случайных последовательностях наблюдений, можно вывести тест на проверку случайности серии. Мы задаем вопрос: Три серии, состоящие из сорока наблюдений, которые мы рассматриваем, слишком ли много это или слишком мало в сравнении с количеством серий, возможном в абсолютно случайной последовательности из 40 наблюдений?

Если в нашем примере больше серий, это значит, что остатки часто меняют знаки, таким образом, указывая на негативную автокорреляцию. Если же серий меньше, то мы можем предполагать наличие положительной автокорреляции. Априори, рис. 9 указывает на положительную автокорреляцию остатков.

Пусть

N = общее количество наблюдений = N ₁ + N ₂

N ₁ = количество знаков +, т.е. положительных остатков

N ₂ = количество знаков –, т.е. отрицательных остатков

R = количество серий

Затем как нулевую гипотезу примем следующий исход — остатки абсолютно случайны, при условии, что N ₁ > 10 и N ₂ > 10, количество серий (асимптотически) нормально распределено с

Математическим ожиданием: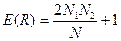

Дисперсией: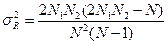

Заметим также, что .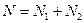

Возвращаясь к нашему примеру, мы знаем что N ₁ — количество минусов равно 19, и N ₂ — количество плюсов равно 21. Количество серий равно 3. Используя формулы, приведенные выше, получаем:

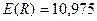
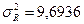
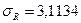
Доверительный интервал 95% для R в нашем примере следующий:

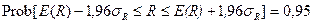
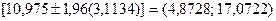
Очевидно, что этот интервал не включает 3. Отсюда, мы можем отклонить гипотезу о том, что остатки нашей регрессии (доходы — продуктивность) на 95% уровне значимости случайны.

Другими словами, в остатках наблюдается автокорреляция. Можно вывести общее правило: если наблюдается положительная автокорреляция, количество серий будет меньшим, а при наличии отрицательной автокорреляции, количество серий будет большим доверительного интервала.

Свед (Sved) и Эйзенхарт (Eisenhart) разработали таблицы, которые дают критические значения серий ожидаемых в случае случайной последовательности из N наблюдений, если N ₁ и N ₂ меньше 20. Используя эти таблицы, читатель может проверить что остатки в нашей регрессии несомненно, неслучайны, в действительности они положительно автокоррелированы. [1]