Жесткости звеньев, соединяющих приведенные массы, также должны быть приведенными.
Рассмотрим систему, состоящую из поступательно движущихся масс (рис. 12а), нагруженных силами 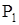 ,
, 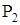 ,
, 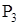 ,
, 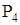 , …,
, …, 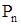 .
.
Если приведение системы производят к массе mП, приведенная жесткость расчетной системы определяется следующим образом.
Статическая сила P1, действующая на массу m1, вызовет перемещение 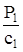 за счет упругой деформации звена c1; перемещение массы m2, соответственно, равно
за счет упругой деформации звена c1; перемещение массы m2, соответственно, равно 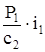 , перемещение следующей массы m3 составит
, перемещение следующей массы m3 составит 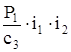 и т.д., т.е. перемещение массы m1 под действием силы P1
и т.д., т.е. перемещение массы m1 под действием силы P1
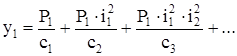 (37)
(37)
Таблица 2
Формулы для определения жесткости элементов систем*
| Схема элемента | Описание элемента | Жесткость, податливость |
| Стержень постоянного сечения (S=const) | 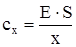 | |
| Плоский стержень трапецеидального профиля (S=var) | 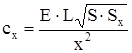 | |
| Ступенчатый стержень | При x=L 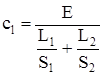 | |
| Консольная балка при I=const | 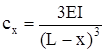 | |
| Консольная балка при Ix=var, I – в сечении заделки | 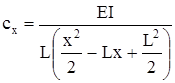 | |
| Консольная балка при Ix=var, I – в сечении заделки | 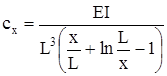 При При 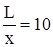 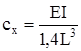 |
* S и I – площадь и момент инерции поперечного сечения соответственно.
Продолжение табл. 2
 | Двухопорная балка при I=const | 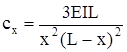 |
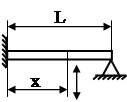 | Двухопорная балка с заделкой одного конца при I=const | 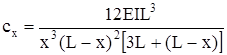 |
 | Балка с жесткой заделкой концов при I=const | 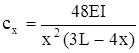 |
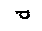  | Вал постоянного диаметра | 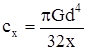 |
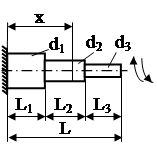 | Ступенчатый вал | 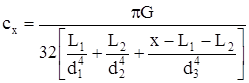 |
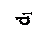 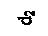 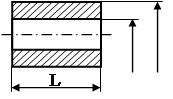 | Полый вал | 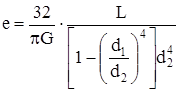 |
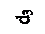 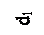 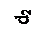 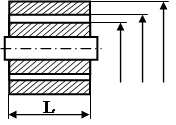 | Деталь типа шкива | 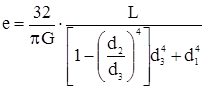 |
Продолжение табл. 2
| Конический вал | 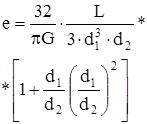 | |
Зубчатое колесо α=20˚ – угол зацепления; z – число зубьев; 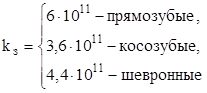 | 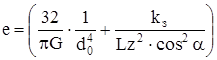 , или , или 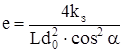 | |
| Муфта: dб – диаметр болта; z – число болтов. | 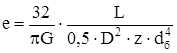 | |
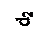 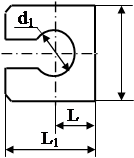 | Вилка универсального шпинделя | 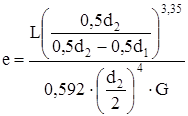 |
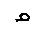 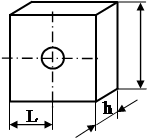 | Прямоугольный элемент γ – коэффициент, учитывающий соотношение b/h | 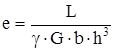 b/h 2,0 2,5 3,0 4,0 γ 0,23 0,25 0,26 0,28 b/h 2,0 2,5 3,0 4,0 γ 0,23 0,25 0,26 0,28 |
 | Плоская пружина: δ – толщина; b – ширина пружины | 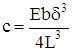 |
Продолжение табл. 2
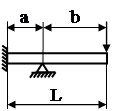 | Плоская пружина с промежуточной опорой | 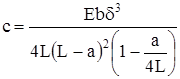 |
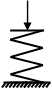 | Цилиндрическая винтовая пружина: D – средний диаметр пружины; d – диаметр проволоки; i – число витков | 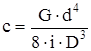 |
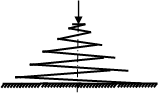 | Коническая винтовая пружина: D и d1 – наибольший и наименьший диаметры пружины; d – диаметр проволоки; i – число витков | 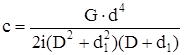 |
 | Мембрана, свободно опертая по периметру: δ – толщина мембраны; ν – коэффициент Пуассона | 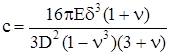 |
 | Мембрана, защемленная по периметру | 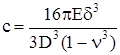 |
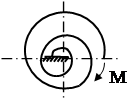 | Спиральная пружина: δ и b – толщина и ширина сечения витков пружины; L – полная длина пружины | 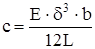 |
 | Винтовая пружина при кручении: D – диаметр пружины; d – диаметр проволоки; i – число витков | 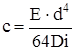 |
Перемещение той же массы m1 под действием силы P2
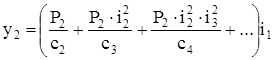 (38)
(38)
и так далее.
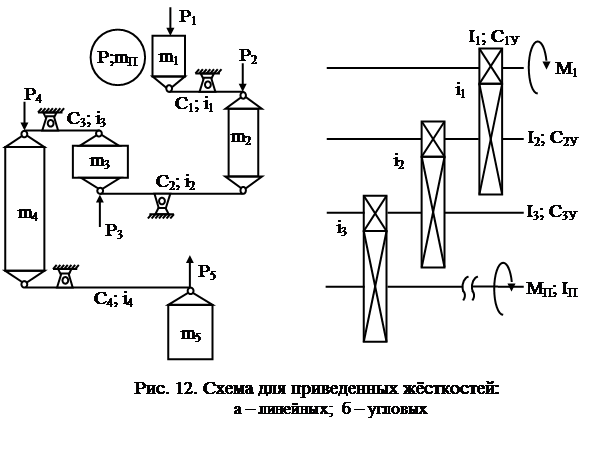
Полная деформация системы, т.е. перемещение массы m1 составит
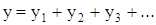 (39)
(39)
Нагрузка системы, приведенная к массе m1(mП),
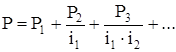 (40)
(40)
Приведенная жесткость системы
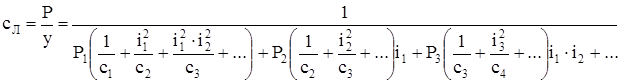 (41)
(41)
Большинство машин воспринимает внешние нагрузки только крайними массами. Для этого случая в формуле (41) все силы, кроме P1, должны быть равны нулю.
Тогда
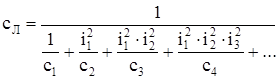 . (42)
. (42)
Для системы с вращающимися массами (рис. 12б) приведенная угловая жесткость равна
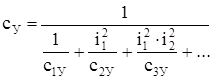 . (43)
. (43)
Если в системе имеются движущиеся поступательно и вращающиеся части (массы), то жесткость может быть представлена либо как линейная, либо как угловая:
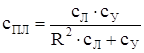 , (44)
, (44)
или
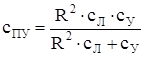 , (45)
, (45)
где R – радиус приведения линейной жесткости к угловой и обратно.
 2015-08-21
2015-08-21 1531
1531
