Вопрос. Критерии и методы оценки инвестиционных проектов

Лекция 15. Методы обоснования реальных инвестиций

Вопросы: 1.Критерии и методы оценки инвестиционных проектов

2. Противоречивость критериев оценки

вопрос. Критерии и методы оценки инвестиционных проектов

Оценка инвестиционного проекта – это некоторая техника обоснования целесообразности и выгодности его реализации. Безусловно, любой проект можно отбирать к реализации, руководствуясь в той ли иной мере интуицией, однако ориентация на методы количественного обоснования, рассматриваемые в данной лекции, представляется более оправданным способом

В основе принятия управленческих решений инвестиционного характера лежит оценка и сравнение объёма предполагаемых инвестиций и будущих денежных поступлений, т. е. необходимо сравнить величину требуемых вложений с прогнозируемыми доходами. Поскольку сравниваемые показатели относятся к разным моментам времени, ключевой проблемой здесь является их сопоставимость.

С формальной точки зрения, любой инвестиционный проект зависит от ряда параметров, которые подлежат оценке и нередко задаются в виде дискретного распределения, что позволяет проводить этот анализ как имитационное моделирование.

В теории и практике инвестиционного анализа разработаны критерии оценки проектов. Под критериями оценки инвестиционных проектов будут пониматься показатели, используемые а) для отбора и ранжирования проекта; б) оптимизации эксплуатации проекта; в) формирования оптимальной инвестиционной программы. Критерии, используемые в анализе инвестиционной деятельности, можно разделить на две группы: основанные на дисконтированных оценках и основанные на учётных оценках. В первом случае во внимание принимается фактор времени, во втором – нет.

В первую группу входят следующие критерии:

Чистая приведённая стоимость (Net Present Value, NPV)

Чистая терминальная стоимость (Net Terminal Value, NTV)

Индекс рентабельности инвестиции (Profitability Index, PI)

Внутренняя норма прибыли (Internal Rate of Return, IRR)

Модифицированная внутренняя норма прибыли (Modified Internal Rate of Return, IRR)

Дисконтированный срок окупаемости инвестиций (Discounted Payback Period, DPP)

Во вторую группу входят:

Срок окупаемости инвестиции (Payback Period, PP)

Учётная норма прибыли (Accounting Rate of Return, ARR)

Используя в практической деятельности эти критерии, следует иметь в виду два обстоятельства 1) ни один критерий не может рассматриваться как безусловный и неоспоримый аргумент. Принятие решения в отношении такого сложного явления, как инвестиционный проект, должно основываться на комплексе доводов, в числе которых могут быть один или несколько формализованных критериев 2) русскоязычная терминология в разделе, посвящённом управлению инвестиционными проектами, не устоялась, поэтому в литературе можно встретить другие варианты наименований критериев; в частности, весьма распространённы названия NPV «чистая приведённая стоимость», «чистый приведённый эффект», «чистая настоящая стоимость» и др.

Рассмотрим идеи, лежащие в основе методов оценки инвестиционных проектов, использующих данные критерии.

Метод расчёта чистой приведённой (дисконтированной) стоимости. Под чистой приведённой стоимостью (Net Present Value, NPV) понимается разность суммы элементов возвратного потока и исходной инвестиции, дисконтированных к началу действия ожидаемого проекта. В основу данного метода заложено следование основной целевой установке – повышение ценности фирмы, количественной оценкой которой служит её рыночная стоимость. Соответственно целесообразность принятия проекта будет зависть от того, будет ли иметь место приращение ценности фирмы в результате реализации проекта.

Метод основан на сопоставлении величины исходной инвестиции (IC) с общей суммой дисконтированных чистых денежных поступлений, генерируемых ею в течение прогнозируемого срока. Поскольку приток денежных средств распределён во времени, он дисконтируется с помощью ставки r, устанавливаемой аналитиком, исходя из ежегодного процента возврата, который он хочет или может иметь на инвестируемый им капитал.

Чистая дисконтированная стоимость рассчитывается по следующей формуле:

n

NPV = ∑[CF_k / (1 + r)^k] – IC (1)

k=1

где CF_k – годовые доходы;

k – порядковый номер года;

r – ставка дисконтирования;

IC – исходная инвестиция.

Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение m лет, то формула для расчёта NPV модифицируется следующим образом:

n m

NPV = ∑[CF_k / (1 + r)^k] – ∑[IC_j/(1 + i)^j] (2)

k=1 j=1

где i – прогнозируемый средний темп инфляции

При расчётах NPV, как правило, используется постоянная ставка дисконтирования, однако при некоторых обстоятельствах (например, ожидается изменение учётных ставок) могут использоваться значения ставки, индивидуализируемые по годам. Если в ходе расчётов приходится применять различные ставки дисконтирования, то применение формулы (2) становится затруднительным, кроме того, проект, приемлемый при постоянной дисконтной ставке, может стать неприемлемым.

Имея в виду упомянутую выше основную целевую установку, на достижение которой направлена деятельность любой компании, можно дать экономическую интерпретацию трактовки критерия NPV с позиции её собственников:

если NPV < 0, то в случае принятия проекта ценность компании уменьшится, поэтому проект следует отклонить;

если NPV > 0, то в случае принятия проекта ценность компании увеличится, поэтому проект следует принять;

если NPV = 0, то в случае принятия проекта ценность компании не изменится, поэтому решение о целесообразности его принятия должно приниматься на основании дополнительных аргументов. В данной ситуации следует иметь в виду, что инвестиционные проекты нередко принимаются управленческим персоналом самостоятельно. Для менеджмента компании проект с NPV = 0 также может быть привлекателен, поскольку ведёт к увеличению масштаба компании: чем крупнее компания, тем престижнее работа, тем труднее разобраться в проблемах новому менеджменту, тем выше жалование (т.к. сложнее работа) и т.д., т.е. существует первый тип агентского конфликта, поэтому собственники компании должны внимательно разобраться, почему менеджмент настаивает на принятии такого проекта.

При прогнозировании доходов по годам необходимо учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с данным проектом. Поступления в виде ликвидационной стоимости оборудования, высвобождения части оборотных средств должны быть учтены как доходы соответствующих периодов. Напротив, если закрытие проекта предполагает затраты по ликвидации связанных с ним последствий (например, восстановление экологии, затраты на вывоз оборудования и т.п.), то они должны быть учтены как отток средств в соответствующем году.

Расчёт с помощью приведённых формул вручную трудоёмок, поэтому для удобства применения методов, основанных на дисконтированных оценках, разработаны финансовые таблицы, финансовые калькуляторы и специальное программное обеспечение для ПК.

Пример. Проанализировать проект со следующими характеристиками (млн. руб.): – 150, 30, 70, 70, 45. Возможны два случая: 1) стоимость капитала 12%; 2) ожидается, что стоимость капитала будет меняться по годам следующим образом: 12%, 13%,14%, 14%.

Решение. Воспользуемся формулой (1)

1) NPV = – 150 + 30/1,12 + 70/1,122 + 70/1,123 + + 45/1,124 = 11,0 млн. руб., NPV > 0, т.е. проект является приемлемым.

2) NPV = – 150 + 30/1,12 + 70/1,12·1,13 + 70/1,12·1,13·1,14 + 45/1,12·1,13·1,14² = – 12,0 млн. руб., NPV < 0, т.е. проект не приемлем.

Метод расчёта чистой терминальной стоимости. Под чистой терминальной стоимостью (Net Terminal Value, NTV) понимается разность суммы элементов возвратного потока и исходной инвестиции, наращённых к моменту окончания оцениваемого проекта. Если в первом методе используется операция дисконтирования, то в данном случае – операция наращения. Формула для расчёта этого критерия имеет следующий вид:

n

NTV = ∑CF_k·(1 + r)^n-k – IC·(1 + r)ⁿ (3)

k=1

Условия принятия проекта на основе критерия NTV такие же, как и NPV: если NTV>0, то проект следует принять, если NTV < 0, то проект следует отклонить, если NTV = 0, то проект ни прибыльный, ни убыточный.

Критерии NPV и NTV взаимообратны:

NTV = NPV(1 + r)ⁿ NPV = NTV/(1 + r)ⁿ (4)

Эти критерии дублируют друг друга, т.е. отбор проекта по одному из них даёт в точности такой же результат при использовании другого критерия. Например, в условиях предыдущего примера по формулам (3) и (4) имеем:

NTV = – 150·1,12⁴ + 30·1,12³ + 70·1,12² + 70·1,12 + 45 = 17,33 млн. руб.

NPV = NTV · 1/(1 + r)ⁿ = 17,33 · 0,6355 = 11,0 млн. руб.

В практической деятельности упор чаще делается на NPV.

Метод расчёта индекса рентабельности инвестиции. Индекс рентабельности инвестиции (Profitability Index, PI) – это отношение суммы дисконтированных элементов возвратного потока к исходной инвестиции. Этот метод по сути является следствием метода расчёта NPV. Индекс рентабельности также предусматривает сопоставление дисконтированных элементов возвратного потока с исходной инвестицией, но в виде не разности, а отношения. Расчёт ведётся по формуле

n

PI ={∑[CF_k / (1 + r)^k]} / IC (5)

k=1

Очевидна логика применения критерия: а) если PI >1, то проект следует принять, если PI<1, то проект следует отвергнуть, если PI = 0, то проект не является ни прибыльным, ни убыточным.

В отличие от NPV индекс рентабельности является относительным показателем: он характеризует уровень доходов на единицу затрат, т.е. эффективность вложений. Чем больше значение этого показателя, тем выше отдача каждого рубля, инвестированного в проект. Благодаря этому критерий PI очень удобен при выборе одного проекта из альтернативных, имеющих примерно одинаковое значение NPV (например, одинаковые NPV, но разные объёмы требуемых инвестиций, очевидно, что выгоден проект с большей эффективностью вложенных средств), либо при комплектовании портфеля инвестиций с целью максимизации суммарного значения NPV. Этот критерий предпочтителен при комплектовании портфеля инвестиций в случае ограничения по объёму источников финансирования. Последовательность действий в этом случае выглядит следующим образом: 1) независимые проекты упорядочивают по убыванию PI; 2) в портфель последовательно включают проекты с наибольшими значениями PI; 3) подтверждают расчётом оптимальность полученного портфеля (с позиции максимизации совокупного NPV).

Метод расчёта внутренней нормы прибыли инвестиции. Внутренняя норма прибыли (Internal Rate of Return, IRR) используется для оценки инвестиции и численно равна значению ставки дисконтирования, при которой чистая дисконтированная (приведённая) стоимость инвестиционного проекта (NPV) равна нулю. Принимается во внимание временная ценность денежных средств. Синонимы: внутренняя норма доходности, внутренняя норма окупаемости. Т.е. IRR это ставка процента r, при которой инвестиционный проект по доходности выходит в ноль.

При определении истинной доходности инвестиций, которые приносят единственный денежный поток через один год, двусмысленности не возникает:

Доходность = Отдача/Инвестиция – 1

Или же мы можем записать формулу чистой приведённой стоимости инвестиций и определить ставку дисконтирования, при которой NPV = 0.

NPV = CF₁/(1 + r) – IC = 0,

тогда:

r = (CF₁/IC) – 1

К сожалению, нет вполне удовлетворительного способа найти истинную доходность долгосрочных активов. Для определения этой величины (IRR) инвестиционного проекта продолжительностью n лет мы должны вычислить IRR из следующего выражения:

NPV = C₁/(1 + IRR) + C₂/(1 + IRR)² + … + C_n/(1 + IRR)ⁿ – IC = 0

Как известно, формулы для вычисления корней подобных уравнений существуют только для уравнений не выше четвёртой степени. Но и эти формулы сложны и далеко не всегда помогают легко находить корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты, поэтому решения уравнений более высокого порядка находятся алгебраическими методами, путём последовательных итераций с помощью вычислительной техники. На практике внутреннюю норму доходности обычно находят методом подбора (один из вариантов будет рассмотрен ниже).

Таким образом, для конкретного проекта значение IRR равняется r, найденному из общего уравнения:

n

NPV = f (r) = 0 или ∑[CF_k / (1 + r) ^k] – IC = 0 (6)

k=1

Формулу NPV более удобно представлять в следующем виде:

n

NPV = f(r) = ∑[CF_k / (1 + r)^k] (7)

k=0

где CF_k – элементы денежного потока проекта;

CF₀ = IC – исходная инвестиция;

n – продолжительность инвестиционного проекта.

Ниже, на рис. 1, приведён график функции y = f(r) = NPV для наиболее типовой ситуации, когда единовременный отток (инвестиция IC) сменяется серией притоков (CF_k), в сумме превосходящих IC. В дальнейшем проект с подобным денежным потоком будем условно именовать классическим проектом.

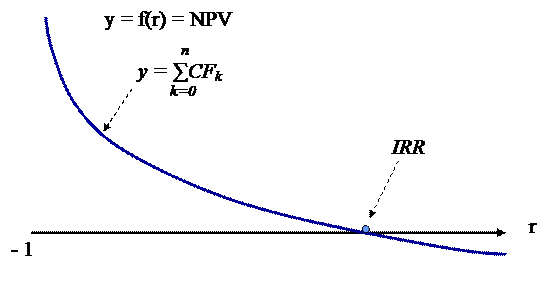
Рис. 1 График NPV типового инвестиционного проекта

Видно, что y = f(r) – нелинейная функция; как будет показано ниже, это свойство может иметь очень серьёзные последствия при расчёте критерия IRR. Для классического инвестиционного проекта функция y является убывающей, т.е. с ростом r график функции стремится к оси абсцисс и пересекает её в точке IRR; для классического проекта характерно однократное пересечение графиком оси абсцисс. Но ввиду нелинейности функции и возможных комбинаций знаков элементов денежного потока функция может иметь несколько точек пересечения с осью абсцисс. График функции стремится к ∞ при приближении r к –1; это формальное свойство, которое не следует интерпретировать в терминах процентных ставок.

Показатель IRR измеряется в процентах и означает максимально допустимый уровень затрат по финансированию проекта, при достижении которого реализация проекта не приносит экономического эффекта, но и не даёт убытка. Таким образом, смысл расчёта IRR, как правило, заключается в слtдующем: IRR показывает нулевую ожидаемую доходность проекта; следовательно максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. Например, если проект полностью финансируется за счёт ссуды, то значение IRR показывает границу банковской процентной ставки, превышение которой делает проект убыточным.

На практике любая коммерческая организация финансирует свою деятельность, в том числе инвестиционную, из разных источников. В качестве платы за пользование авансированными ресурсами она уплачивает проценты, дивиденды, вознаграждения и т.п., т.е. несёт некоторые расходы. Показатель, характеризующий относительный уровень этих расходов в отношении долгосрочных источников средств, как было показано ранее, называется средневзвешенной стоимостью капитала (WACC). Этот показатель отражает сложившийся в коммерческой организации минимум возврата на вложенный в её деятельность капитал, его минимально необходимую рентабельность.

Таким образом, экономический смысл критерия IRR заключается в следующем: коммерческая организация может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя «стоимость капитала» (Cost of Capital, CC), под которым понимается либо WACC, если источник не идентифицирован, либо стоимость целевого источника. Именно с показателем СС сравнивается IRR, рассчитанный для конкретного проекта, при этом связь между ними такова:

а) если IRR>CC, то проект следует принять; б) если IRR<CC, то проект следует отвергнуть; в) если IRR=CC, то проект не является ни прибыльным, ни убыточным.

Независимо от того с чем сравнивается IRR, очевидно одно: проект принимается, если его IRR больше некоторой пороговой величины; поэтому при прочих равных условиях, как правило, большее значение IRR считается предпочтительным.

Показатель IRR даёт характеристику резерва безопасности. При высоком значении IRR можно быть относительно спокойным в отношении точности прогнозных оценок дохода: если, скажем, значения ожидаемых доходов (особенно последних периодов) были завышены, значение IRR может снизиться (например, с 60% до 45%), но всё ещё оставаться высоким для нормального уровня процентных ставок (в нормальной экономике уровни затрат имеют вполне определённые ориентиры и не могут быть катастрофически высокими, например, выше 40%)

Значение IRR, как было отмечено выше, находят с помощью финансового калькулятора или персонального компьютера. Если технические средства отсутствуют можно воспользоваться методом линейной аппроксимации, предусматривающим нахождение IRR путём последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью финансовых таблиц выбирают два значения ставки дисконтирования r₁ < r₂ таким образом, чтобы в интервале (r₁, r₂) функция NPV (r), т.е. значение NPV для данной ставки r, меняла своё значение с «+» на «–», или с «–» на «+». Далее применяют формулу:

IRR' = r₁ + {NPV(r₁)/[NPV(r₁) – NPV(r₂)]}(r₁ – r₂), (8)

где r₁ - значение табулированной ставки дисконтирования, при которой NPV(r₁) > 0 (NPV(r₁) < 0),

r₂ - значение табулированной ставки дисконтирования, при которой NPV(r₂) < 0 (NPV(r₂) > 0)

Пример. Определить значение IRR для проекта рассчитанного на 3 года, требующего инвестиций в размере 10 млн. руб. и имеющего предполагаемые денежные поступления в размере 3 млн. руб., 4 млн. руб., 7 млн. руб.

Решение. Возьмём два произвольных значения ставки дисконтирования: r = 10%, r = 20%. Соответствующие расчёты с использованием значений 1/(1 + r)^k, найденных по финансовой таблице 2 Приложения 3 (Ковалёв В.В. Финансовый менеджмент, стр. 1001), приведены в таблице 1 ниже (значения величин 1/(1 + r)^k можно, естественно, рассчитывать, а не находить с помощью таблиц).

Сначала находим значения множителя 1/(1 + r)ⁿ для каждого года и для значения r=10% (по таблице 2 приложения 3, либо по приведённой формуле) и вписываем их в колонку «Расчёт 1». Для нулевого года, т.е. для начала вложения средств, это множитель равен 1, т.к. денежные потоки будут приводиться к этому моменту. После этого денежные потоки каждого года (3,4,7 млн. руб.) приводятся к моменту вложения средств по формуле: CF_k·[1/(1 + r)^k], т.е. умножением величины соответствующего денежного потока на значение найденного множителя (3·0,909 = 2,73; 4·0,828 = 3,30; 7·0,751 = 5,26). Значения найденных приведённых потоков денежных средств вписываются в колонку PV (Present Value), после чего вычисляется значение NPV = –10 + (2,73 + 3,30 + 5,26) = 1,29 млн. руб. Это NPV для величины r = 10%. Таким же образом вычисляется чистая дисконтированная стоимость для r = 20%: NPV = – 0,67. Теперь по формуле (7) вычисляем значение IRR в первом приближении:

IRR = 0,1 + {1,29/[1,29 – (– 0,67)]}·(0,2 -0,1) = 0,166 = 16,6%

Можно уточнить полученное значение. Допустим, что путём последующих итераций мы определили ближайшие целые значения ставки дисконтирования, при которых NPV меняет знак (столбец «Вторая итерация) и рассчитали, что при r = 16% NPV = +0,05, а при r = 17% NPV = – 0,14. тогда уточнённое значение IRR будет равно:

IRR = 0,16 + {0,05/[0,05 – (– 0,14)]}·(0,17 -0,16) = 0,1626 = 16,26%

Истинное значение показателя IRR в данном случае равно 16,23%, т.е. метод последовательных итераций в силу гладкости функции NPV обеспечивает весьма высокую точность (отметим, что с практической точки зрения такая точность является излишней). Иными словами, если взять в расчёт два значения r, то можно «накрыть» этим интервалом значение IRR с первой итерации, т.е. получит вполне приемлемое значение критерия. Вычисления приведены в таблице 1.

Таблица 1