· Закон Кулона
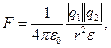
где 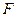 – модуль силы взаимодействия двух точечных зарядов
– модуль силы взаимодействия двух точечных зарядов 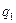 и
и 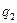 в вакууме;
в вакууме; 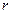 – расстояние между зарядами;
– расстояние между зарядами; 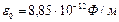 – электрическая постоянная;
– электрическая постоянная; 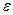 - диэлектрическая проницаемость вещества (для вакуума
- диэлектрическая проницаемость вещества (для вакуума 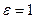 )
)
· Напряженность и потенциал электростатического поля
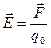 ;
; 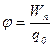 , или
, или 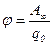 ,
,
где 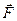 - сила, действующая на точечный положительный заряд
- сила, действующая на точечный положительный заряд 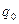 , помещенный в данную точку поля;
, помещенный в данную точку поля; 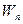 - потенциальная энергия заряда
- потенциальная энергия заряда 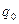 в электростатическом поле;
в электростатическом поле; 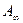 - работа по перемещению заряда
- работа по перемещению заряда 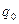 из данной точки поля за пределы поля.
из данной точки поля за пределы поля.
· Напряженность и потенциал электростатического поля точечного заряда 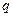 на расстоянии
на расстоянии 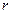 от заряда
от заряда
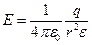 ;
; 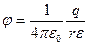 .
.
· Поток вектора напряженности через площадку 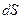
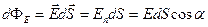 ,
,
где 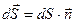 - вектор, модуль которого равен
- вектор, модуль которого равен 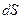 , а направление совпадает с нормалью
, а направление совпадает с нормалью 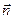 к площадке;
к площадке; 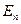 – составляющая вектора
– составляющая вектора 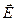 по направлению нормали
по направлению нормали 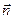 к площадке (
к площадке (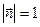 );
); 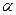 -угол между векторами
-угол между векторами 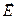 и
и 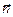 .
.
· Поток вектора напряженности через произвольную поверхность 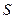
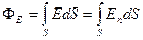 .
.
· Поток вектора напряжённости через замкнутую поверхность (рис. 14)
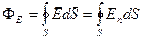 .
.
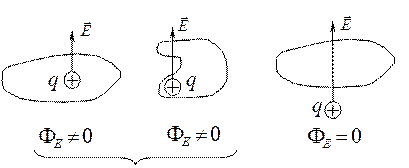
Рис.14.
· Принцип суперпозиции (наложения) электростатических полей
 ;
; 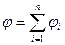
 ,
,
где 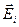 ,
, 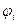 - соответственно напряженность и потенциал поля, создаваемого зарядом
- соответственно напряженность и потенциал поля, создаваемого зарядом 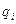 .
.
· Направление вектора напряжённости 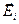 , создаваемого точечным зарядом
, создаваемого точечным зарядом 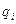 (рис. 15):
(рис. 15):
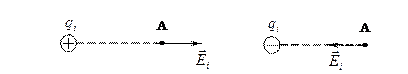
Рис.15
Напряженность электрического поля, созданного двумя разноимёнными зарядами в точках А, В и С (рис. 16):
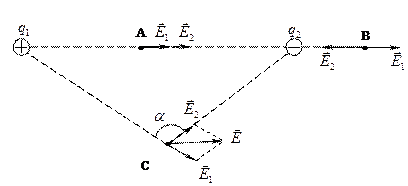
Рис.16.
В точке А: 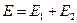 .
.
В точке В: 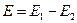 .
.
В точке С: 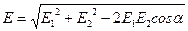 .
.
· Связь между напряженностью и потенциалом электростатического поля
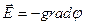 , или
, или 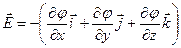 ,
,
где 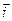 ,
,  ,
, 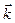 - единичные векторы координатных осей. Знак минус определяется тем, что вектор напряженности
- единичные векторы координатных осей. Знак минус определяется тем, что вектор напряженности 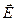 поля направлен в сторону убывания потенциала (рис. 17).
поля направлен в сторону убывания потенциала (рис. 17).
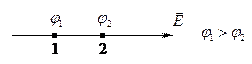
Рис.17.
· Направление вектора градиента потенциала в точке А (рис.18):

Рис.18.
· В случае поля, обладающего центральной или осевой симметрией
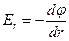 .
.
· Эквипотенциальные поверхности – геометрическое место точек с одинаковым потенциалом. Вектор напряжённости направлен по нормали к эквипотенциальной поверхности.
· Электрический момент диполя (дипольный момент)
 ,
,
где 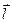 - плечо диполя (рис. 19).
- плечо диполя (рис. 19).
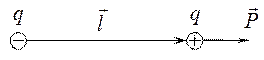
Рис.19.
Напряженность поля на продолжении оси диполя на расстоянии от центра диполя 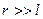
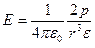 ,
,
Напряженность поля на перпендикуляре, восстановленном к оси диполя из ее середины на расстоянии 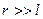
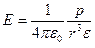 .
.
· Линейная, поверхностная и объемная плотности зарядов, т.е. заряд, приходящийся соответственно на единицу длины, поверхности и объема:
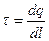 ;
; 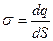 ;
; 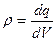 .
.
· Теорема Гаусса для электростатического поля в вакууме
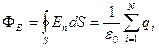 ,
,
где 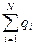 - алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности
- алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности 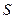 ;
; 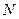 – число зарядов.
– число зарядов.
Если заряд распределён внутри замкнутой поверхности непрерывно с объёмной плотностью 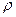 , то
, то
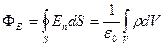
Примеры. 1. Определить поток 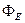 вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечный заряд
вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечный заряд 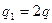 (рис. 20).
(рис. 20).
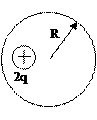
Рис.20.
По теореме Гаусса
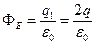 .
.
2. Как изменится поток через ту же поверхность, если внутрь поместить ещё один заряд 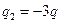 (рис. 21)?
(рис. 21)?
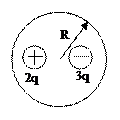
Рис.21.
По теореме Гаусса
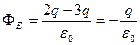 ,
,
т.е. поток уменьшится вдвое и станет отрицательным.
3. Как изменится поток через данную поверхность, если около неё поместить любой заряд 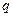 на расстоянии
на расстоянии 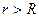 (рис. 22)?
(рис. 22)?
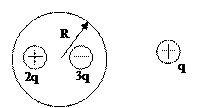
Рис.22.
Поток не изменится, так как заряд находится вне поверхности.
· Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью,
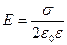 .
.
· Напряжённость поля, создаваемого двумя бесконечными параллельными разноимённо заряженными плоскостями:
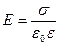 – между плоскостями;
– между плоскостями;
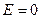 – вне плоскостей.
– вне плоскостей.
· Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом 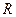 с общим зарядом
с общим зарядом 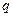 на расстоянии
на расстоянии 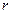 от центра сферы,
от центра сферы,
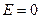 при
при 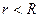 (внутри сферы);
(внутри сферы);
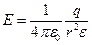 при
при 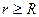 (вне сферы).
(вне сферы).
· Напряженность поля, создаваемого объемно заряженным шаром радиусом R с общим зарядом q на расстоянии r от центра шара,
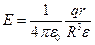 при
при 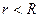 (внутри шара);
(внутри шара);
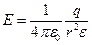 при
при 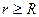 (вне шара).
(вне шара).
· Напряженность поля, создаваемого равномерно заряженным проводящим бесконечнодлинным цилиндром (нитью) радиусом 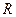 на расстоянии
на расстоянии 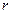 от оси цилиндра,
от оси цилиндра,
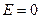 при
при 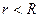 (внутри цилиндра);
(внутри цилиндра);
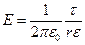 при
при 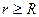 (вне цилиндра).
(вне цилиндра).
· Работа, совершаемая силами электростатического поля при перемещении заряда 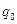 из точки 1 в точку 2,
из точки 1 в точку 2,
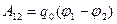 , или
, или 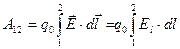 ,
,
где 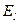 – проекция вектора
– проекция вектора 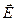 на направление элементарного перемещения
на направление элементарного перемещения 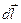 ;
; 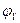 и
и 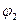 – потенциалы электростатического поля в точках 1 и 2.
– потенциалы электростатического поля в точках 1 и 2.
· Работа сил электростатического поля не зависит от вида траектории, а определяется только начальным и конечным положениями точки, по замкнутому пути работа равна нулю.
· Циркуляция вектора напряжённости электростатического поля вдоль замкнутого контура равна нулю, следовательно, это поле потенциальное
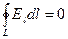 .
.
Линии напряжённости электростатического поля начинаются и заканчиваются на зарядах.
· Вектор поляризации диэлектрика:
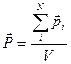 ,
,
где 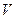 - объем диэлектрика;
- объем диэлектрика; 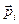 - дипольный момент
- дипольный момент 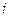 -й молекулы;
-й молекулы; 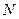 - число молекул диэлектрика в объеме
- число молекул диэлектрика в объеме 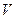 .
.
· Связь между векторами поляризации и напряженности электростатического поля внутри диэлектрика
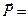 æ
æ 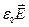 ,
,
где æ – диэлектрическая восприимчивость вещества.
· Связь диэлектрической проницаемости e с диэлектрической восприимчивостью æ
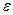 = 1+æ.
= 1+æ.
· Связь между напряженностью 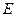 поля в диэлектрике и напряженностью
поля в диэлектрике и напряженностью 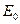 внешнего поля
внешнего поля
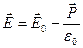 , или
, или 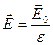 .
.
· Связь между векторами электрического смещения (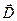 ) и напряжённостью электростатического поля (
) и напряжённостью электростатического поля (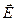 ):
):
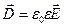
· Связь между 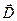 ,
, 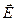 и
и 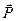 :
:
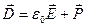 .
.
· Теорема Гаусса для электростатического поля в диэлектрике
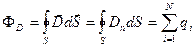 ,
,
где 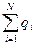 – алгебраическая сумма свободных электрических зарядов, заключенных внутри замкнутой поверхности
– алгебраическая сумма свободных электрических зарядов, заключенных внутри замкнутой поверхности 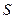 ;
; 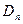 – составляющая вектора
– составляющая вектора 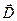 по направлению нормали
по направлению нормали 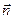 к площадке
к площадке 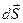 ;
; 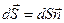 – вектор, модуль которого равен
– вектор, модуль которого равен 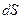 , а направление совпадает с нормалью
, а направление совпадает с нормалью 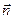 к площадке. Интегрирование ведется по всей поверхности.
к площадке. Интегрирование ведется по всей поверхности.
· Электроемкость уединенного проводника и конденсатора:
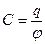 ,
, 
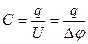 ,
, 
где 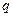 – заряд, сообщенный проводнику;
– заряд, сообщенный проводнику; 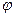 – потенциал проводника;
– потенциал проводника; 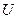 ,
, 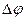 – разность потенциалов между пластинами.
– разность потенциалов между пластинами.
· Электроемкость шара
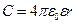 ,
,
где r – радиус шара.
· Электроемкость плоского конденсатора
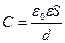 ,
,
где 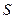 – площадь пластины конденсатора;
– площадь пластины конденсатора; 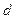 – расстояние между пластинами.
– расстояние между пластинами.
· Электроемкость цилиндрического конденсатора
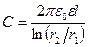 ,
,
где 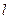 – длина обкладок конденсатора;
– длина обкладок конденсатора; 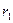 и
и 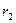 - радиусы внутренней и внешней обкладок конденсатора.
- радиусы внутренней и внешней обкладок конденсатора.
· Электроемкость сферического конденсатора
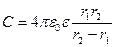 ,
,
где 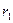 и
и 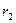 - радиусы сферических обкладок конденсатора.
- радиусы сферических обкладок конденсатора.
· Электроемкость системы конденсаторов соответственно при последовательном (а) и параллельном (б) соединениях:
а) 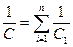 ;
;
б) 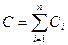 ,
,
где 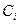 – электроемкость
– электроемкость 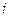 – го конденсатора;
– го конденсатора; 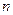 - число конденсаторов.
- число конденсаторов.
· Энергия уединенного заряженного проводника
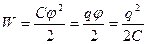 .
.
· Потенциальная энергия системы точечных зарядов
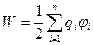 ,
,
где 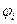 – потенциал, создаваемый в той точке, где находится заряд
– потенциал, создаваемый в той точке, где находится заряд 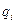 всеми зарядами, кроме
всеми зарядами, кроме 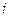 -го.
-го.
· Энергия заряженного конденсатора
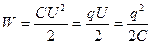 ,
,
где 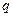 – заряд конденсатора;
– заряд конденсатора; 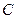 – его емкость;
– его емкость; 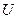 – разность потенциалов между обкладками.
– разность потенциалов между обкладками.
· Сила притяжения между обкладками плоского конденсатора
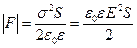 .
.
· Энергия электростатического поля плоского конденсатора
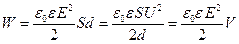 ,
,
где 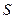 – площадь одной пластины;
– площадь одной пластины; 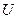 – разность потенциалов между пластинами;
– разность потенциалов между пластинами; 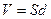 – объем области между пластинами конденсатора.
– объем области между пластинами конденсатора.
· Объемная плотность энергии электростатического поля
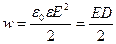 ,
,
где 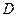 – электрическое смещение;
– электрическое смещение; 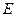 - напряжённость поля.
- напряжённость поля.
· Если конденсатор заряжен до разности потенциалов (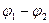 ) и отключен от источника тока, то при изменении расстояния между пластинами заряд на них неизменен, т.е.
) и отключен от источника тока, то при изменении расстояния между пластинами заряд на них неизменен, т.е. 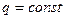 .
.
Если конденсатор не отключен от источника тока, то при изменении расстояния между пластинами неизменна разность потенциалов, т.е. 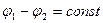 .
.
 2015-09-07
2015-09-07 281
281








