Векторний добуток двох векторів

Векторним добутком двох векторів 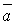і 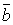називається вектор , який задовольняє таким умовам:

1) Довжина вектора дорівнює площі паралелограма, побудованого на векторах 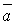і 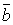, тобто

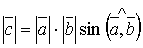(37).

2) Вектор перпендикулярний до площини цього паралелограма, тобто перпендикулярний і до вектора 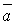, і до вектора :

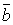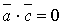та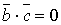

3) Вектори 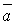, , 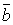, взяті у такому порядку, утворюють праву трійку векторів. Упорядкована трійка некомпланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого здійснюється проти обертання годинникової стрілки.

Для векторного добутку вектора 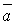на вектор 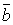вводиться позначення:

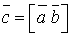або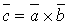

Якщо вектори-множники взаємно перпендикулярні, то модуль векторного добутку дорівнює добутку модулів співмножників:

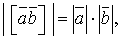якщо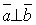

Якщо вектори-множники колінеарні, то 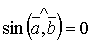і векторний добуток їх дорівнює нуль-вектору, тобто

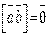
Закон комутативності для векторного добутку 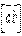не виконується, або точніше вектор 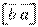має напрям, протилежний до :

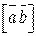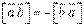
Властивість сполучності відносно скалярного множника зберігається:

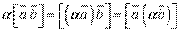
Властивість розподільності для векторного добутку також зберігається:

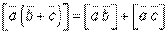
Якщо векторний добуток двох векторів записати у координатній формі, то маємо:

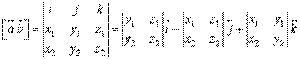(45).

Якщо 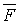є вектор сили, прикладеної до деякої точки В, а вектор 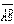, спрямований з точки А в точку В, то векторний добуток 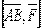буде моментом 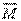сили 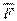відносно точки А.