Екстремум функції. Необхідна умова існування екстремуму. Достатні умови екстремуму

Екстремум-найбільше і найменше значення функції. Необхідна умова екстремуму: Якщо ф-я z=f(x;у)має в точці (х₀;у₀) локальний(місцевий) екстремум, то в цій точці частинні похідні першого порядку на змінних х,та у = 0 або не існують.

Нехай функція 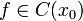неперервна в 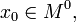і існують кінцеві або безкінечніодносторонні похідні 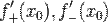. Тоді за умови 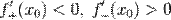,х₀ є точкою строгого локального максимуму. А якщо 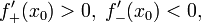то х₀ є точкою строгого локального мінімуму. Зауважимо, що при цьому функція не дифференцируема в точці х₀ Нехай функція f неперервна і двічі диференційована в точці. х₀ Тоді за умови 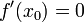і 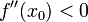, х₀ є точкою локального максимуму. А якщо 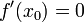і 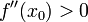то х₀ є точкою локального мінімуму.