Математика колебания струны и тайны гармонии

В 1747 г. Жан ле Рон Д’Аламбер (1717 — 1783), французский математик, философ, писатель, один из создателей знаменитой «Энциклопедии наук, искусств и ремесел», член Парижской и Петербургской Академий, опубликовал статью «Исследование по вопросам о кривой, которую образует натянутая струна, приведенная в колебание», где впервые задача о колебании струны сводилась к решению дифференциального уравнения в частных производных, названного волновым уравнением:

Здесь t — время; x — координата струны в положении равновесия; 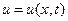— неизвестная функция, выражающая отклонение точки с координатой x в момент времени t от положения равновесия; 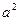— коэффициент пропорциональности, характеризующий упругие свойства струны (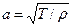; T — сила натяжения струны; ρ — плотность однородной струны). Символы 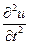и 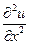обозначают частную производную второго порядка, которая определяется как производная от производной (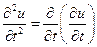).·Частные производные 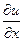и 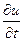, как и обыкновенная производная 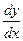, характеризуют скорость изменения функции 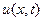по каждой из переменных x или t в отдельности при условии, что другая переменная не изменяется. Предполагается, что струна совершает малые колебания, происходящие в одной плоскости.

Еще через полвека другой соотечественник Д’Аламбера Жан Батист Жозеф Фурье (1768 — 1830), выдающийся математик и сподвижник императора Наполеона, изобрел новый метод, позволивший получить общее решение задачи о колебании конечной струны. Эта задача формулируется так: найти решение волнового уравнения (3.3.1), удовлетворяющее начальным и граничным условиям:

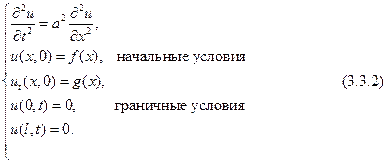
Начальные условия означают, что в момент времени 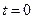струне придали некоторую форму 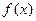и сообщили ускорение 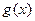. Граничные условия показывают, что на концах 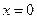или 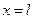струна жестко закреплена.

Опуская промежуточные выкладки, выпишем решение Фурье задачи о колебании конечной струны, которое представляет собой бесконечную сумму слагаемых, или, как говорят, разложение функции 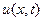в ряд:

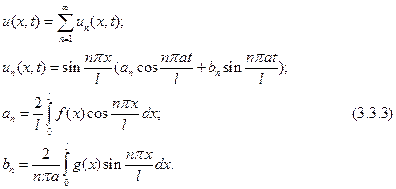
Выясним физический смысл решения (3.3.3), и прежде всего функций 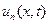, составляющих это решение. Для этого выполним искусственное преобразование:

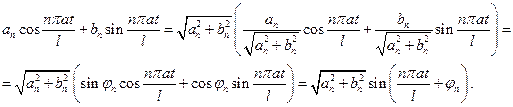
Итак,

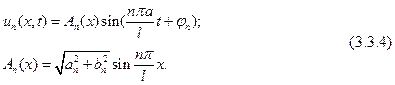
Из формулы (3.3.4) видно, что каждое решение 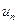представляет собой гармоническое колебание (т. е. колебание по закону синуса) с одной и той же частотой 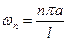и фазой 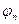. Амплитуда же колебаний 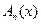для разных точек струны разная. Ясно также, что пр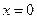и и 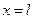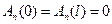, т. е. на концах струна неподвижна. Итак, во времени колебания струны происходят с постоянной частотой 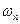, но с переменной по координате x амплитудой. При этом все точки струны одновременно достигают своего максимального отклонения в одну или другую сторону и одновременно проходят положения равновесия. Такие колебания называют стоячими волнами. Пользуясь выражением для амплитуды стоячей волны (3.3.4) и учитывая, что 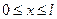, найдем неподвижные точки стоячих волн:

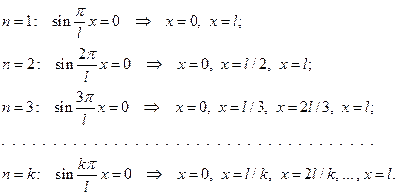
Неподвижные точки называются узлами стоячей волны. Ясно, что посередине между узлами расположены точки, в которых отклонения в стоячей волне достигают максимума. Эти точки называются пучностями стоячей волны.

Сделаем общий вывод: колебание конечной струны представляет собой бесконечную сумму стоячих волн 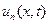, каждая из которых имеет постоянную частоту колебания 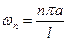и переменную по длине струны амплитуду 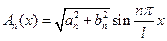. В k -й стоячей волне имеется k пучностей и 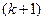узлов. На рисунке 77 показаны четыре первые стоячие волны струны.

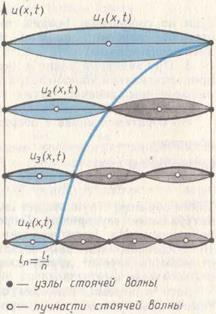
Рис. 77. Четыре первые стоячие волны (гармоники) колеблющейся струны.

Перейдем теперь к «музыкальному содержанию» решения (3.3.3). Мы пришли к выводу, что струна колеблется не только всей своей длиной, но одновременно и отдельными частями: половинками, третями, четвертями и т. д. Следовательно, струна издает звук не только основной частоты 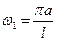, но и призвуки частот 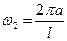, , 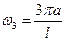…, , …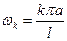. Тон основной частоты струны 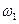называется основным тоном струны, а остальные тона, соответствующие частотам 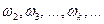, называются обертонами (верхними тонами) или гармониками. Основной тон струны принимается за первый обертон. Именно обертоны, сливаясь в общем звучании с основным тоном, который имеет наибольшую амплитуду и потому наиболее заметен, придают звуку музыкальную окраску, называемую тембром.

Различие тембров музыкальных звуков прежде всего объясняется составом и интенсивностью обертонов у разных источников звуков. Чем больше у звука обертонов, тем красивее, «богаче» он нам кажется. По тембру, т. е. по составу обертонов, мы отличаем звуки одной и той же высоты и одинаковой громкости, воспроизводимые на скрипке или фортепьяно, голосом или на флейте.

Рассмотрим подробнее основной тон струны. Вспоминая, что 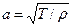, получим формулу для частоты основного тона:

откуда легко увидеть законы колебания струны, которые экспериментально пытались обнаружить на монохорде пифагорейцы. А именно:

1. Для струн одинаковой плотности и одинакового натяжения частота колебания обратно пропорциональна длине струны (это в точности пифагорейский закон (3.1.2)).

2. При заданной длине и плотности струны ее частота пропорциональна корню квадратному из натяжения (этот закон, судя по сообщению Боэция, пифагорейцы знали только качественно, ошибочно полагая высоту тона пропорциональной натяжению струны).

3. При заданной длине и натяжении частота струны обратно пропорциональна корню квадратному из ее плотности (этот закон пифагорейцы, конечно, также могли знать только качественно: чем толще струна, тем ниже издаваемый ею звук).

Но обратимся вновь к обертонам. Легко видеть, что частоты обертонов 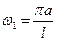, , 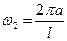…, , … 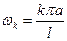относятся как числа натурального ряда:

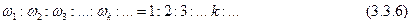
Таким образом, струна издает целый звукоряд тонов, называемый натуральным звукорядом. Теоретически натуральный звукоряд бесконечен. На практике же имеют значение лишь первые 16 обертонов, так как остальные обертоны слишком мало отличаются друг от друга, обладают слишком малой энергией и фактически не слышны.

Зато в первых, наиболее сильных обертонах мы находим замечательное свойство: второй обертон с основным тоном образует интервал октавы 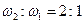, третий и второй обертоны—интервал квинты 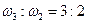, четвертый и третий — кварты 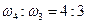. Но ведь это есть не что иное, как набор совершенных консонансов! Причем у второй гармоники с первой совпадает каждый второй узел стоячей волны, у третьей с первой — каждый третий, а у четвертой с первой — каждый четвертый (рис. 77). Ясно, что, чем больше узлов у двух стоячих волн совпадает, тем они «больше похожи» друг на друга, т. е. тем созвучнее образуемый ими интервал. Следовательно, с ростом номера гармоники степень консонантности интервала убывает.

Итак, мы приходим к разгадке закона целочисленных отношений консонансов (3.1.1), который, по преданию, был экспериментально открыт самим Пифагором. Все совершенные консонансы, т. е. интервалы с отношением частот вида 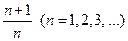, определены самой природой колебания струны. Все совершенные консонансы заключены в первых четырех, наиболее мощных гармониках колеблющейся струны, причем по мере удаления от первой гармоники (основного тона) степень консонантности интервала убывает. Этот «закон консонансов» является следствием математического решения задачи о колебании конечной струны (3.3.3).

Со временем в теории музыки стали различать и несовершенные консонансы: большую и малую терции. Эти интервалы как среднее арифметическое и среднее гармоническое основного тона (1) и квинты (3/2) нашел еще Архит. В самом деле, для интервального коэффициента большой терции имеем

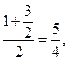
а для интервального коэффициента малой терции:

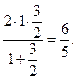
Легко видеть, что несовершенные консонансы определяются следующими — пятой и шестой — гармониками колеблющейся струны. По этому поводу еще в XVIII в. французский музыкальный теоретик Балльер с присущей французу легкостью писал: «Разница между древностью и современностью заключается в том, что тогда начинали считать диссонансы с 5-го призвука, а теперь начинают их считать лишь с 7-го».

Но почему именно шесть гармоник определяют все консонансы? Почему знаменитый «фальшивый», седьмой, обертон не входит ни в какие музыкальные созвучия, тогда как девятый и восьмой образуют основу всей музыкальной гаммы — известный нам тон-интервал (9/8)? Эти и немало других вопросов все еще остаются тайнами гармонии.

В заключение заметим, что пифагорейцы имели практически такое же объяснение явлению консонансов, которое следует из решения (3.3.3). Начиная с Архита греки представляли звук как совокупность множества отдельных ритмических ударов струны по воздуху и таких же колебаний воздуха. Тогда в консонансе октавы отдельные удары верхнего тона происходят в два раза чаще, чем у более низкого основного тона. Следовательно, каждый второй удар верхнего тона достигает нашего уха одновременно с одним ударом основного тона, при этом основной тон как бы целиком переходит в верхний и сливается с ним в едином звучании. В консонансе квинты каждый третий удар верхнего тона совпадает с каждым вторым ударом основного тона, и поэтому квинта звучит менее слитно, чем октава. И так далее. Но совпадение числа ударов струны по воздуху эквивалентно совпадению числа узлов в стоячей волне, которые и определяют число таких ударов в единицу времени, т. е. частоту колебания струны.

Таким образом, пифагорейцы совершенно правильно представляли себе физические основы явления консонанса! Мы же имеем еще одну возможность убедиться в блестящей интуиции и глубоком проникновении пифагорейцев в суть физических явлений.

Начиная с Пифагора теории музыки посвящали глубокие исследования такие прославленные ученые, как Архит и Евклид, Клавдий Птолемей и Северин Боэций, а впоследствии Иоганн Кеплер, Готфрид Лейбниц, Леонард Эйлер. Не всегда эти изыскания приносили желанные плоды (так, о математической теории музыки Эйлера говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов), но всегда они служили развитию как науки математики, так и искусства музыки. И в математике, и в музыке продолжали звучать могучие аккорды, некогда взятые Пифагором.

На этом мы расстаемся с пифагорейской теорией музыки. Но расстаемся ненадолго, ибо пифагорейская музыка продолжала звучать в... пифагорейской астрономии.