Стійкість за першим наближенням

Систему рiвнянь

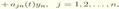
називають системою першого наближення, а задачу на стiйкiсть точки спокою цiєї системи – задачею на стiйкiсть розв’язку в першому наближенi.Розглянемо окремий випадок системи

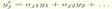
i дослiдимо питання про стiйкiсть тривiального розв’язку системи. Розв’язки цiєї системи мають вигляд

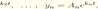k1, k2,..., kn – характеристичнi числа системи, а для iснування нетривiальних розв’язкiв необхiдно й досить, щоб

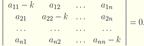
Розглянемо окремi випадки, пов’язанi з виглядом коренiв рiвняння

1. Якщо всi характеристичнi числа системи мають вiд’ємнi дiйснi частини, то тривiальний розв’язок системи асимптотично стiйкий.

2. Якщо хоча б одне характеристичне число системи має додатну дiйсну частину (тобто або це число додатне, або комплексне з додатноюдiйсною частиною), то тривiальний розв’язок системи нестiйкий.

3. Якщо серед характеристичних чисел системи немає чисел з додатними дiйсними частинами, але є простi числа з нульовоюдiйсною частиною, то тривiальний розв’язок системи є стiйким, але не асимптотично стiйким.

4. Якщо серед характеристичних чисел системи немає чисел з додатними дiйсними частинами, але є кратнi числа з нульовими дiйсними частинами, то можливi як стiйкi,

так i нестiйкi тривiальнi розв’язки.

Теорема 1. Нехай функцiї Rj(t, y1,..., yn),j = 1-n неперервнi за сукупнiстю змiнних i нескiнченно малi вище першого порядку при yi → 0, i = 1-n, тобто для всiх (t=> t0) i (|yi| < d) |Rj(t, y1,..., yn)| <= M(|y1|1+α + |y2|1+α + …+ |yn|1+α), j = 1-n, або |Rj(t, y1,..., yn)| <=ω(y)|y|, j = 1, 2,..., n,

де |y| =sqrt(y1^2+ y2^2+… yn^2), α,M – додатнi сталi, ω(y) → 0 при |y| → 0. Нехай, крiм того, ajk(t) = ajk, j, k = 1, 2,..., n, де ajk – сталi. Тодi якщо характеристичнi числа системи мають вiд’ємнi дiйснi частини, то розв’язок системи асимптотично стiйкий; якщо хоча б одне характеристичне число має додатну дiйсну частину, то розв’язок системи нестiйкий.