2015-09-06
514
Интенсивными называются свойства, значение которых не зависит от массы (удельные свойства, температура, давление и т.д.), экстенсивными называются те свойства, значение которых зависит от массы системы (масса, объем, энергия, энтальпия). Химическое превращение – процесс преобразования одних компонентов в другие. При этом происходит изменение чисел молей компонентов.
Изменение экстенсивного свойства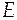 
при постоянных давлении и температуре за счет протекания химической реакции находится по формуле
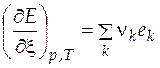, (5.1)
где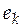 
− парциальное мольное экстенсивное свойство компонента k в реакционной смеси.
После интегрирования (5.1) можно найти интегральное изменение экстенсивного свойства Е. Обычно парциальное мольное свойство вещества k представляют как
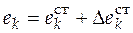, (5.2)
где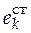 
– стандартное мольное свойство вещества 
;
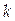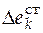– изменение стандартного мольного свойства за счет образования смеси реагирующих веществ.
Стандартное свойство вещества k характеризует данное вещество в стандартном состоянии. В соответствии с рекомендациями ИЮПАК стандартное состояние вещества выбрано следующим образом: температура вещества в стандартном состоянии равна температуре системы; давление над веществом (или давление газообразного вещества) равно 1 бар (105 Па). Следовательно, понятие стандартного мольного свойства системы никак не связано с какой-либо конкретной температурой. Исторически сложилось так, что для единообразия справочных данных стандартные мольные величины стали определять и табулировать при давлении 1 атм и температуре 298 К. Именно эти условия стали называть стандартными условиями.
Первое слагаемое в уравнении (5.2) зависит только от давления и температуры, а второе слагаемое зависит от концентрации раствора.
Если в качестве стандартного мольного свойства использовать мольное свойство Е компонента в виде чистого вещества (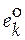
), то второе слагаемое уравнения (5.2) будет соответствовать парциальной мольной функции смешения (
)
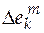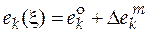. (5.3)
Известно, что обычно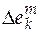 
<< 
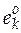, поэтому в уравнении (5.3) часто учитывают только стандартную часть, и подстановка полученного выражения в (5.1) приводит к выражению для расчета изменения экстенсивного свойства за счет протекания химической реакции
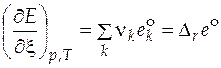, (5.4)
где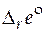 
− стандартное мольное свойство Е реакции.
В справочниках приводятся значения стандартных мольных энтропий чистых веществ при температуре 298 К и давлении 1 атм (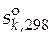
). Эти данные позволяют рассчитать стандартное мольное изменение энтропии реакции при температуре 298 К
.
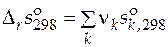Стандартные мольные энтальпии и функции Гиббса чистых веществ найти невозможно, т.к. нельзя определить абсолютное значение внутренней энергии вещества, а следовательно, и любых других термодинамических функций, включающих внутреннюю энергию. Поэтому для расчета стандартной мольной теплоты реакции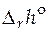 
обычно прибегают к линейным комбинациям стандартных мольных энтальпий других реакций. Так, например, стандартную мольную энтальпию реакции A + 2B = C находят как комбинацию реакций образования компонентов реакции (химических соединений) из простых веществ
,
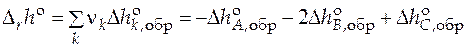где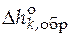 
– стандартная мольная теплота реакции образования вещества k.
Справочники содержат данные по 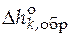при температуре 298 К и давлении 1 атм. Это позволяет рассчитать стандартную мольную теплоту любой реакции при этих условиях:
.
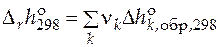Для расчета стандартных мольных энтропий и энтальпий реакций при любых температурах, отличных от 298 К, нужно располагать данными о зависимости стандартной мольной изобарной теплоемкости реакции от температуры. Эта зависимость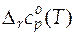 
в общем виде дается следующим степенным рядом
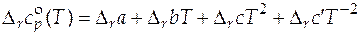, (5.5)
где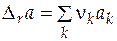 
; 
; 
; 
.
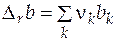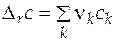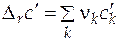Уравнение для расчета стандартного мольного изменения энтальпии в ходе химического превращения называется уравнением Кирхгофа:
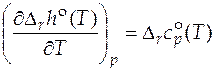. (5.6)
Разделяя переменные и проводя интегрирование, можно получить
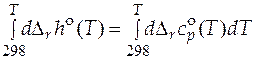. (5.7)
=
.
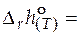
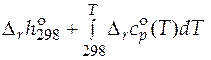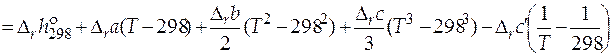Расчет стандартной мольной энтропии реакции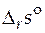 
при произвольной температуре T основан на соотношении:
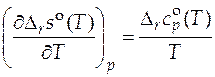. (5.8)
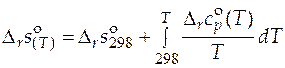. (5.9)
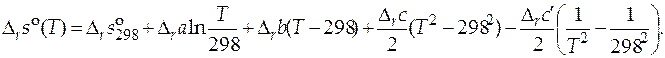
Зная функци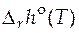и 
и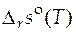 
, можно рассчитать значение стандартного мольного изменения энергии Гиббса в ходе химической реакции 
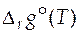при любой температуре. Определив стандартную мольную энергию Гиббса в результате протекания химической реакции при различных температурах процесса, можно вычислить величины констант химического равновесия данной реакции при этих же температурах
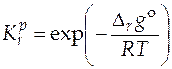. (5.10)
Знание константы равновесия реакции позволяет рассчитать состав равновесной системы, т.е. определить максимально возможный, или теоретический, выход желаемого продукта. Для этого необходимо решить уравнение закона действия масс (закона химического равновесия). В предположении идеального поведения газов оно примет вид
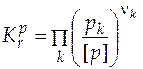, (5.11)
где давление выражено как отношение парциального давления к единице размерности давления, т.е. оно не имеет размерности.
Парциальное давление каждого участника реакции по закону Дальтона равно произведению общего давления и мольной доли компонента Nk
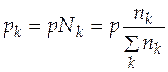. (5.12)
Если теперь выразить числа молей всех компонентов через начальное количество и глубину реакции, то при известном общем давлении в системе и известной величине константы равновесия будем иметь одно уравнение с одной неизвестной величиной – глубиной реакции:
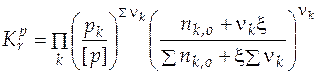. (5.13)
Для газовой реакции, если газы близки к идеальным,известно уравнение изотермы химической реакции
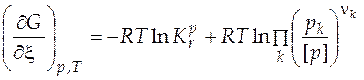, (5.14)
которое позволяет определить возможность протекания процесса в том или ином направлении при известных начальных условиях.
Количественно зависимость константы равновесия от температуры описывается уравнением изобары химической реакции (изобара Вант-Гоффа)
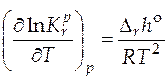(дифференциальная форма);
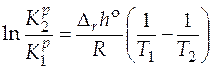(интегральная форма). (5.15)
По этому уравнению, зная константы равновесия при двух разных температурах, можно рассчитать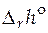 
реакции. Зная 
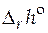реакции и константу равновесия при одной температуре, можно рассчитать константу равновесия при другой температуре. А в случае, когда известны величины констант равновесия при нескольких температурах, строят графическую зависимость 
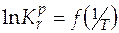. Угловой коэффициент получаемой прямой позволит определить величину стандартной мольной энтальпии реакции.
