Краткая теория и методика выполнения работы

Наука, изучающая процессы, возникающие при нарушениях равновесия системы, носит название физической кинетики. При нарушении равновесия система стремится вернуться в равновесное состояние. При этом возникают так называемые явления переноса, в результате которых в физической системе происходит направленный пространственный перенос электрического заряда, массы, плотности, концентрации, импульса, энергии или какой-либо другой физической величины. Такие процессы являются необратимыми и сопровождаются возрастанием энтропии.

В термодинамике изучают следующие явления переноса: вязкость (или внутреннее трение) – перенос импульса, теплопроводность – перенос кинетической энергии и диффузию – перенос вещества. В простейшем случае явления переноса одномерны – определяющие их физические величины зависят только от одной декартовой координаты.

На основе молекулярно-кинетической теории вещества можно получить общее уравнение переноса, описывающее все три перечисленных выше явления.

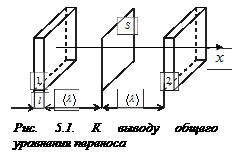Пусть сквозь площадку 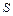(рис. 5.1) в результате хаотического движения молекул переносится некоторая физическая величина. На расстояниях 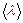, равных средней длине свободного пробега молекул, справа и слева от площадки 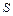выделим прямоугольные параллелепипеды малой толщины 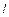(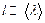). Внутри каждого параллелепипеда содержится 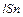молекул, где 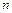– концентрация молекул вещества.

В следствие равновероятного движения молекул по всем направлениям, в направлении 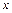перпендикулярном площадке 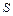со стороны объема 1 будет перемещаться 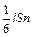молекул. Так как объем 1 находится на расстоянии 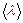, то эти молекулы будут двигаться до площадки 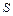без соударений. Такое же число 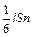молекул достигнет площадки 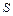в обратном оси 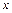направлении от объема 2.

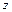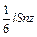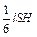Каждая молекула переносит некоторую величину (масса, импульс, кинетическая энергия), а все молекулы в выделенном объеме переносят или , где 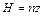– физическая величина, переносимая молекулами, заключенными в единице объема. В результате сквозь площадку 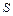из объемов 1 и 2 за промежуток времени 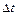переносится физическая величина, равная:

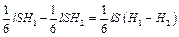. (5.1)

Считают, что все молекулы движутся с одинаковыми средними скоростями 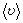. Тогда молекулы из объемов 1 и 2, достигшие площадки 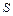, пересекают ее в течение времени 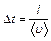. Тогда значение переносимой величины в единицу времени можно найти так:

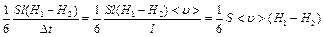. (5.2)

Изменение величины 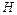на единицу длины, то есть 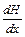, есть градиент величины 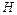вдоль направления 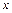. Так как изменение этой величины происходит на расстоянии 2 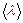, то:

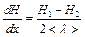или 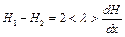. (5.3)

Подставив (5.3) в (5.2) и умножив обе части полученного уравнения на время, найдем поток 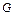переносимой физической величины 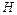за промежуток времени 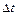сквозь площадку 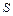в направлении оси :

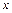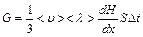. (5.4)

Уравнение (5.4) получено без предположения в каком из объемов 1 или 2 концентрация молекул, переносящих физическую величину, больше. Но перенос физической величины всегда происходит в направлении ее убывания, а градиент величины будет направлен противоположно соответствующему потоку, что в аналитической записи отражается знаком «минус». Введем его в уравнение (5.4). Получим:

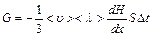. (5.5)

Это общее уравнение переноса, используемое при изучении явлений диффузии, вязкости и теплопроводности.

В данной работе изучается явление диффузии. Диффузия (от лат. diffusion – распространение, растекание) – взаимное проникновение соприкасающихся веществ друг в друга вследствие теплового движения частиц вещества. Диффузия происходит в направлении уменьшения концентрации вещества и ведет к его равномерному распределению по занимаемому объему.

Диффузия имеет место в газах, жидкостях и твердых телах, причем диффундировать могут как находящиеся в них частицы посторонних веществ, так и собственные частицы (самодиффузия). Наиболее быстро диффузия происходит в газах, медленнее – в жидкостях, еще медленнее – в твердых телах, что обусловлено характером теплового движения частиц в этих средах.

Траектория движения каждой частицы газа представляет собой ломаную линию, так как в столкновениях она меняет направление и скорость движения. Поэтому диффузионное проникновение значительно медленнее свободного движения. Сме­щение частицы 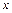меняется со временем случайным образом, но его средний квадрат 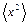за большое число столкновений растет пропорционально времени 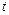: . Коэффициент пропорциональности 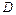называется коэффициентом диффузии. Это соотношение, полученное А. Эйнштейном, справед­ливо для любых процессов диффузии. Для простейшего случая самодиффузии в газах коэффициент диффузии может быть определен, если за среднее смещение принять среднюю длину свободного про­бега молекулы 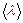. Для газа 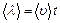,где 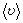– средняя скорость движения частиц, 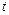– среднее время между столкновениями. Таким образом, 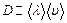. Коэффициент диффузии обратно про­порционален давлению 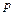газа (так как 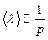). С ростом температуры 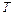( при постоянном объёме) коэффициент 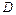увеличивается пропорционально 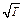, таккак 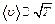. С увеличением молярной массы 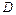умень­шается.

Рассмотрим подробнее диффузию в газах.

Пусть в газе, заполняющем пространство, находится другой газ, концентрация и парциальная плотность (то есть плотность, которую имел бы данный газ в выделенном объеме в отсутствии других газов) которого изменяются вдоль некоторой оси. Следовательно, сквозь площадку 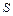, перпендикулярную выбранной оси, в одном направлении будет наблюдаться больший поток молекул второго газа, чем в противоположном направлении. Если в общее уравнение переноса (5.5) вместо потока 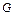подставить величину переносимой массы 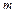диффундирующего газа, а вместо 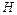– его парциальную плотность, то получим уравнение диффузии:

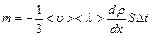. (5.6)

Уравнение (5.6) хорошо согласуется с полученным эмпирическим путем в 1885 г. немецким физиком Адольфом Фиком уравнением для массы газа, переносимой при диффузии сквозь площадку 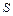за время :

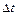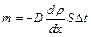, (5.7)

где 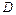– коэффициент диффузии.

Это выражение называют первым законом Фика для диффузии.

Сравнивая уравнения (5.6) и (5.7), получаем формулу для определения коэффициента диффузии:

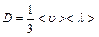. (5.8)