Рациональные, иррациональные, показательные, логарифмические, тригонометрические уравнения
В заданиях В7 предложены несложные рациональные, иррациональные, показательные, логарифмические или тригонометрические уравнения.
При выполнении операций над любыми уравнениями, которые могут привести к новому уравнению, неравносильному исходному уравнению, помните, что:
1) сокращение обеих частей уравнения на множитель, содержащий неизвестное, может привести к потере корней уравнения;
2) при возведении обеих частей уравнения в квадрат (вообще в четную степень), а также при умножении на множитель, содержащий неизвестное и обращающийся в нуль при действительных значениях неизвестного, могут появляться посторонние корни.
Рациональные уравнения
Уравнение f(x) = g(x) называется рациональным, если f(x) и g(x) – рациональные выражения. Если f(x) и g(x) – целые выражения, то уравнение называется целым. Например, целыми являются линейные, квадратные уравнения.
Если же хотя бы одно из выражений f(x), g(x) является дробным, то рациональное уравнение f(x) = g(x) называется дробным (или дробно-рациональным).
В7. Найдите корень уравнения 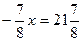 . Решение: . Решение: 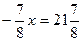 ; ; 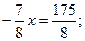 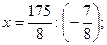 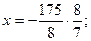 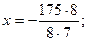 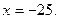 В бланк ответов: В7 В бланк ответов: В7
|
Пример 1 (Линейное уравнение).
Пример 2 (Квадратное уравнение).
В7.Найдите корень уравнения х2 - 13х + 36 = 0. Если уравнение имеет более одного корня, укажите меньший из них. Решение: Здесь а = 1, b = -13, с = 36. Имеем 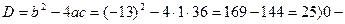 2 корня, которые найдем по формуле: 2 корня, которые найдем по формуле: 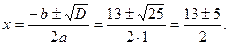 Итак, Итак, 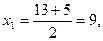 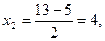 т.е. т.е. 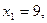 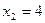 -корни заданного уравнения. Меньший из них 4. В бланк ответов: В7 -корни заданного уравнения. Меньший из них 4. В бланк ответов: В7 |
Чтобы решить дробно-рациональное уравнение, нужно:
1) найти общий знаменатель всех имеющихся дробей;
2) заменить данное уравнение целым, умножив обе его части на общий знаменатель;
3) решить полученное целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
 2015-09-06
2015-09-06 1667
1667