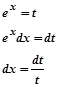Означення. Рівняння
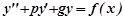 , (7.34)
, (7.34)
де 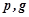 - сталі числа,
- сталі числа, 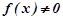 , називається лінійним неоднорідним диференціальним рівнянням другого порядку з сталими коефіцієнтами.
, називається лінійним неоднорідним диференціальним рівнянням другого порядку з сталими коефіцієнтами.
За теоремою про структуру розв’язку лінійного неоднорідного
рівняння другого порядку загальний розв’язок рівняння (7.34) є сумою загального розв’язку відповідного однорідного рівняння і будь-якого частинного розв’язку неоднорідного рівняння. Це твердження записано формулою (7.28): 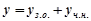 .
.
Загальний розв’язок однорідного рівняння ми детально розглянули вище. Тепер перейдемо до знаходження частинного розв’язку неоднорідних рівнянь із спеціальною правою частиною, розв’язок яких можна знайти не вдаючись до інтегрування.
1) Нехай права частина рівняння (7.34) має вигляд 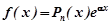 , де
, де 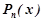 - многочлен n -го степеня. Тут можливі два випадки:
- многочлен n -го степеня. Тут можливі два випадки:
а)  - не є коренем характеристичного рівняння, тоді
- не є коренем характеристичного рівняння, тоді 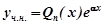 , де
, де 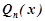 - многочлен n -го степеня із неозначеними коефіцієнтами.
- многочлен n -го степеня із неозначеними коефіцієнтами.
б)  - є коренем характеристичного рівняння кратності
- є коренем характеристичного рівняння кратності 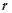 (
(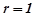 або
або 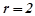 ), тоді
), тоді 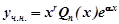 .
.
Зауваження. Якщо 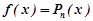 , то вважаємо, що
, то вважаємо, що 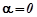 і перевіряємо, чи 0 є коренем характеристичного рівняння.
і перевіряємо, чи 0 є коренем характеристичного рівняння.
Приклад 1. Знайти загальний розв’язок рівняння
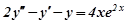 . (7.35)
. (7.35)
Розв’язування. Загальний розв’язок шукаємо у вигляді 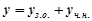 .
.
Спочатку знайдемо загальний розв’язок 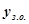 відповідного однорідного рівняння:
відповідного однорідного рівняння:
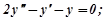
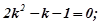
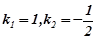 ,
, 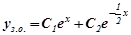 .
.
Частинний розв’язок 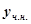 неоднорідного рівняння шукаємо у вигляді правої частини рівняння, а саме
неоднорідного рівняння шукаємо у вигляді правої частини рівняння, а саме 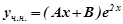 , оскільки
, оскільки 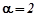 не є коренем характеристичного рівняння. Тут потрібно знайти неозначені коефіцієнти
не є коренем характеристичного рівняння. Тут потрібно знайти неозначені коефіцієнти 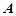 та
та 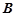 . Для цього знайдемо
. Для цього знайдемо 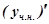 та
та 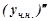 , маємо:
, маємо:
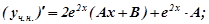
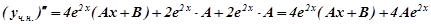 Підставляємо
Підставляємо 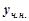 ,
, 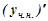 та
та 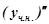 у рівняння (7.35), одержимо
у рівняння (7.35), одержимо 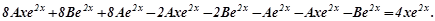 Розділимо ліву і праву частини рівняння на
Розділимо ліву і праву частини рівняння на 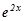 , маємо:
, маємо:
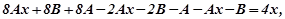
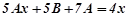 .
.
Відомо, що многочлени рівні між собою тоді і тільки тоді, коли рівні їх коефіцієнти при однакових степенях 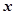 лівої і правої частини, тобто
лівої і правої частини, тобто
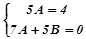 , звідки
, звідки 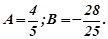
Отже, 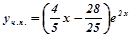 і загальний розв’язок буде
і загальний розв’язок буде 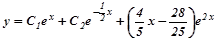 .
.
Приклад 2. Знайти розв’язок диференціального рівняння
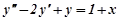 , (7.36)
, (7.36)
який задовольняє початковим умовам 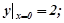
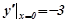 .
.
Розв’язування. Тут характеристичне рівняння 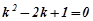 має дійсні, рівні корені
має дійсні, рівні корені 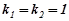 , тому загальний розв’язок відповідного однорідного рівняння буде
, тому загальний розв’язок відповідного однорідного рівняння буде 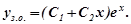
Права частина рівняння (7.36) має вигляд 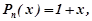 причому
причому 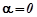 не є коренем характеристичного рівняння, тому частинний розв’язок рівняння будемо шукати у вигляді
не є коренем характеристичного рівняння, тому частинний розв’язок рівняння будемо шукати у вигляді 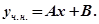 Продиференціювавши
Продиференціювавши 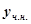 , підставимо у рівняння (7.36), маємо:
, підставимо у рівняння (7.36), маємо:
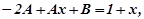 звідки
звідки 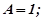
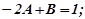
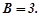
Частинним розв’язком заданого рівняння є функція 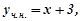 а його загальним розв’язком функція
а його загальним розв’язком функція
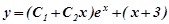 .
.
Знайдемо тепер частинний розв’язок рівняння (7.36), який задовольняє заданим початковим умовам. Для цього знайдемо
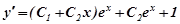 , тоді
, тоді
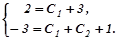 Звідки
Звідки 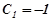 ,
, 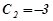 .
.
Шуканим частинним розв’язком буде 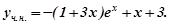
Приклад 3. Розв’язати диференціальне рівняння:
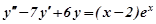 .
.
Розв’язування. Знайдемо загальний розв’язок відповідного однорідного рівняння: 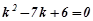 ,
, 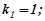
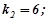
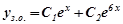 .
.
Частинний розв’язок неоднорідного рівняння шукаємо у вигляді 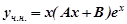 , бо
, бо 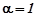 є коренем характеристичного рівняння. Виконавши необхідні обчислення, знайдемо
є коренем характеристичного рівняння. Виконавши необхідні обчислення, знайдемо
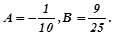 Тоді
Тоді 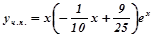 .
.
Отже, загальний розв’язок заданого рівняння буде
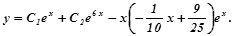
2) Нехай права частина рівняння (7.34) має вигляд
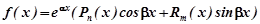 .
.
Перевіряємо чи α + β і є коренем характеристичного рівняння:
а) α + β і не є коренем характеристичного рівняння, тоді 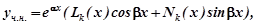 ,
,
де Lk(x), Nk(x), - многочлени k -го степеня з неозначеними коефіцієнтами (k=max(m,n)).
б) α + β і є коренем характеристичного рівняння, тоді 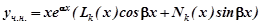 .
.
Зауваження 1. Якщо α=0, то перевіряємо, чи β є коренем характеристичного рівняння.
Зауваження 2. Якщо в правій частині є одна із тригонометричних функцій, наприклад, cosx, то в частинний розв’язок повинна входити і функція sinx.
Приклад4. Розв’язати диференціальне рівняння:
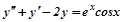 . (7.37)
. (7.37)
Розв’язування. Складаємо характеристичне рівняння і
розв’язуємо його: 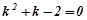 ;
; 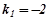 ,
, 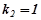 .
.
Загальний розв’язок однорідного рівняння 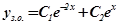 . Права частина неоднорідного рівняння f(x)=excosx, тобто має вигляд
. Права частина неоднорідного рівняння f(x)=excosx, тобто має вигляд
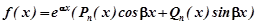 ,
,
де 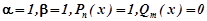 .
.
Оскільки α + β і=1+і не є коренем характеристичного рівняння, а 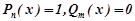 многочлени нульового степеня, то
многочлени нульового степеня, то 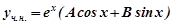 .
.
Знайдемо 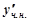 та
та 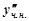 :
:
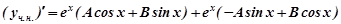
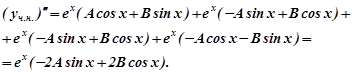
Підставляємо 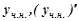 та
та 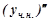 у рівняння (7.37):
у рівняння (7.37):
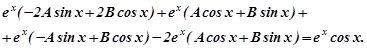
Скорочуючи обидві частини рівності на 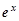 і зводячи подібні члени, одержимо:
і зводячи подібні члени, одержимо:
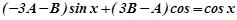
Зрівнюючи коефіцієнти при 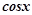 та
та 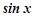 в обох частинах рівняння, одержимо:
в обох частинах рівняння, одержимо:
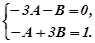 Звідки
Звідки 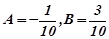 .
.
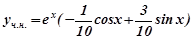 .
.
Загальний розв’язок рівняння (7.37) буде:
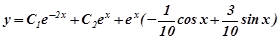 .
.
Приклад 5. Розв’язати рівняння 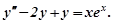
Розв’язування. 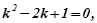
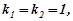
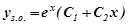 .
.
f(x)=xex, α =1. Число 1- двократний корінь характеристичного рівняння. Отже, r=2.
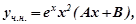 або
або 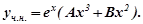
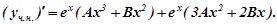
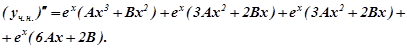
Підставляємо 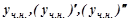 в дане рівняння:
в дане рівняння:
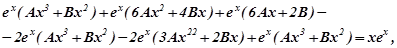
або 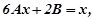 звідси
звідси 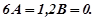
Отже, 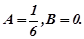 Тому
Тому 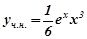 ,
,
а 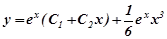 - загальний розв’язок даного диференціального рівняння.
- загальний розв’язок даного диференціального рівняння.
Приклад 6. Розв’язати рівняння 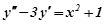 .
.
Розв’язування. 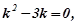
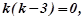
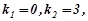
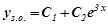 .
.
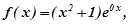
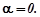 Число
Число 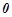 - корінь характеристичного рівняння, тому r=1.
- корінь характеристичного рівняння, тому r=1.
Отже, 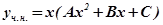 або
або 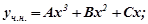
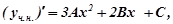
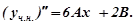
Підставляємо 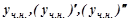 в дане рівняння:
в дане рівняння:
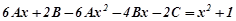 або
або 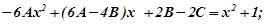
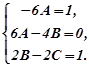
Звідси 
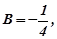
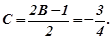
Отже, 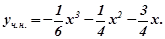
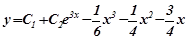 - загальний розв’язок даного рівняння.
- загальний розв’язок даного рівняння.
Приклад 7. Знайти частинний розв’язок рівняння
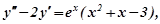 що задовольняє початковим умовам
що задовольняє початковим умовам
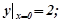
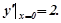
Розв’язування. Шукаємо спочатку загальний розв’язок даного рівняння. Для цього знайдемо уз.о. та уч.н.:
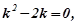
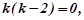
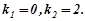
Тому 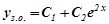 .
.
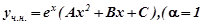 - не є коренем
- не є коренем
характеристичного рівняння).
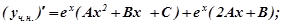
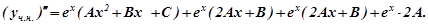
Підставляємо 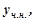
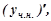
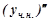 у дане рівняння, одержимо:
у дане рівняння, одержимо:
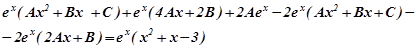
або 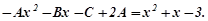
Звідси 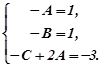
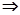
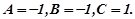
Отже, 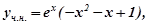
а 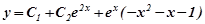 - загальний розв’язок даного рівняння.
- загальний розв’язок даного рівняння.
Розв’яжемо задачу Коші.
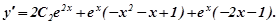
Використовуємо початкові умови
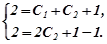
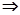
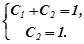
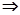
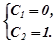
Отже, 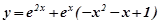 - шуканий частинний розв’язок даного диференціального рівняння, який задовольняє заданим початковим умовам.
- шуканий частинний розв’язок даного диференціального рівняння, який задовольняє заданим початковим умовам.
Приклад 8. Розв’язати рівняння 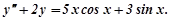
Розв’язування. 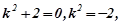
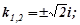
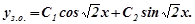
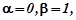
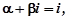
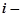 не є коренем характеристичного рівняння. Тому
не є коренем характеристичного рівняння. Тому 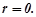
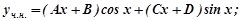
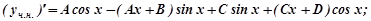
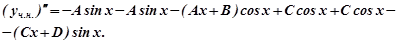
Підставляємо 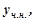
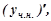
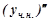 у дане рівняння, одержимо:
у дане рівняння, одержимо:
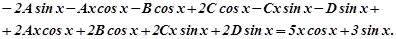
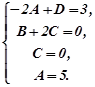
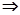
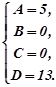 .
.
Таким чином, 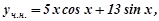 а загальний розв’язок
а загальний розв’язок 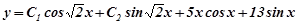 .
.
Ми розглянули метод неозначених коефіцієнтів для відшукання частинного розв’язку лінійних неоднорідних диференціальних рівнянь другого порядку з сталими коефіцієнтами із спеціальною правою частиною.
Розглянемо приклад, коли частинний розв’язок рівняння не можна знайти методом неозначених коефіцієнтів.
Приклад 9. Розв’язати методом варіації довільних сталих рівняння 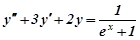 .
.
Розв’язування. Шукаємо загальний розв’язок відповідного однорідного рівняння. Характеристичне рівняння має вигляд k2+3k+2=0, корені якого k1=−2;k2=−1, тому загальний розв’язок однорідного рівняння запишеться: 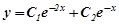 .
.
Покладемо 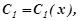
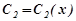 і запишемо систему рівнянь:
і запишемо систему рівнянь:
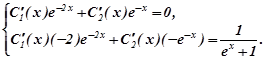
Розв’язуємо систему рівнянь відносно 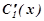 і
і 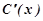 .З першого рівняння:
.З першого рівняння: 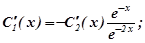
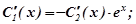
Підставимо 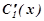 в друге рівняння, маємо:
в друге рівняння, маємо:
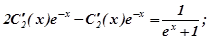
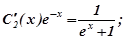
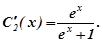
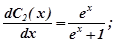
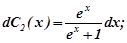
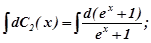
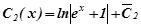 .
.
Тоді, аналогічно, знайдемо 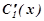 і відповідно
і відповідно 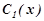 :
:

|
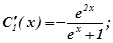
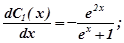
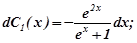
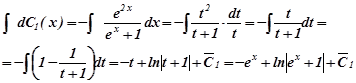
Підставимо знайдені 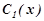 і
і 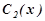 в загальний розв’язок однорідного рівняння, одержимо загальний розв’язок даного неоднорідного рівняння:
в загальний розв’язок однорідного рівняння, одержимо загальний розв’язок даного неоднорідного рівняння:
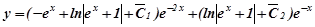 або
або
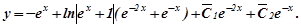
 2015-10-16
2015-10-16 10827
10827