Первичные описательные статистики

К первичным описательным статистикам {Descriptive Statistics) обычно от­носят числовые характеристики распределения измеренного на выборке при­знака. Каждая такая характеристика отражает в одном числовом значении свой­ство распределения множества результатов измерения: с точки зрения их расположения на числовой оси либо с точки зрения их изменчивости. Основ­ное назначение каждой из первичных описательных статистик — замена мно­жества значений признака, измеренного на выборке, одним числом (напри­мер, средним значением как мерой центральной тенденции). Компактное описание группы при помощи первичных статистик позволяет интерпрети­ровать результаты измерений, в частности, путем сравнения первичных ста­тистик разных групп.

МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ

Мера центральной тенденции {Central Tendency) — это число, характеризую­щее выборку по уровню выраженности измеренного признака.

Существуют три способа определения «центральной тенденции», каждо­му из которых соответствует своя мера: мода, медиана и выборочное среднее.

Мода {Mode) — это такое значение из множества измерений, которое встре­чается наиболее часто. Моде, или модальному интервалу признака, соответ­ствует наибольший подъем (вершина) графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным.

ПРИМЕР_______________________________________________________________

Среди 8 значений признака (3, 7, 3, 5, 7, 8, 7, 6) мода Мо = 7 как наиболее часто встречающееся значение. В табл. 3.2 предыдущего параграфа Мо = 3, а в табл. 3.3 модальным является интервал 50—54.

ГЛАВА 4. ПЕРВИЧНЫЕ ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ

Когда два соседних значения встречаются одинаково часто и чаще, чем любое другое значение, мода есть среднее этих двух значений.

Распределение может иметь и не одну моду. Когда все значения встреча­ются одинаково часто, принято считать, что такое распределение не имеет моды.

Бимодальное распределение имеет на графике распределения две вершины, даже если частоты для двух вершин не строго равны. В последнем случае вы­деляют большую и меньшую моду. Во всей группе может быть и несколько локальных вершин распределения частот. Тогда выделяют наибольшую моду и локальные моды.

Еще раз отметим, что мода — это значение признака, а не его частота.

Медиана {Median) — это такое значение признака, которое делит упорядо­ченное (ранжированное) множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая — больше. Таким обра­зом, первым шагом при определении медианы является упорядочивание (ран­жирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом:

□ если данные содержат нечетное число значений (8, 9, 10, 13, 15), то ме­
диана есть центральное значение, т. е. Md= 10;

□ если данные содержат четное число значений (5, 8, 9, 11), то медиана
есть точка, лежащая посередине между двумя центральными значения­
ми, т. е. М/=(8+9)/2 = 8,5.

Среднее (Mean) (М_х — выборочное среднее, среднее арифметическое) — определяется как сумма всех значений измеренного признака, деленная на количество суммированных значений.

Если некоторый признак X измерен в группе испытуемых численностью N, мы получим значения: х_и х₂,..., x_h..., x_N (где / — текущий номер испытуе­мого, от 1 до N). Тогда среднее значение М_х определяется по формуле:

М_х= — Ух,. (4.1)

Свойства среднего. Если к каждому значению переменной прибавить одно и то же число с, то среднее увеличится на это число (уменьшится на это чис­ло, если оно отрицательное):

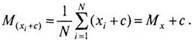1 ^N
^(*,₊O=-^-I>;+c) = M_x+c. ₍₄.2)

А если каждое значение переменной умножить на одно и то же число с, то среднее увеличится в с раз (уменьшится в с раз, если делить на с):

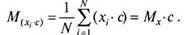M_(XrC)=^i(x_rc)=M_x-c. (4.3)

Далее мы неоднократно будем обращаться к такой величине, как отклоне­ние от среднего: (*,•— М_х). Из первого, очевидного свойства среднего следует

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

еще одно важное свойство, не столь очевидное: сумма всех отклонений от сред­него равна нулю:

£(*,.-Л/_х) = 0. (4.4)

Соответственно, среднее отклонение от среднего также равно 0.

ВЫБОР МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ

Каждая мера центральной тенденции обладает характеристиками, кото­рые делают ее ценной в определенных условиях.

Для номинативных данных, разумеется, единственной подходящей мерой центральной тенденции является мода, или модальная категория — та града­ция номинативной переменной, которая встречается наиболее часто.

Для порядковых и метрических переменных, распределение которых уни­модальное и симметричное, мода, медиана и среднее совпадают. Чем больше отклонение от симметричности, тем больше расхождение между значениями этих мер центральной тенденции. По этому расхождению можно судить о том, насколько симметрично или асимметрично распределение.

Наиболее очевидной и часто используемой мерой центральной тенденции является среднее значение. Но его использование ограничивается тем, что на величину среднего влияет каждое отдельное значение. Если какое-нибудь зна­чение в группе увеличится на с, то среднее увеличится на c/N. Таким образом, среднее значение весьма чувствительно к «выбросам» — экстремально малым или большим значениям переменной.

На величину моды и медианы величина каждого отдельного значения не влияет. Например, если в группе из 20 измерений переменной наибольшее значение утроится по величине, то не изменится ни мода, ни медиана. Вели­чина среднего при этом заметно изменится. Иначе говоря, мода и медиана не чувствительны к «выбросам».

Их средний доход -1000$ в месац...

ПРИМЕР

Если 9 человек имеют месячный доход от 5000 до 6000 рублей, со средним 5600 руб­лей, а доход десятого составляет 15000 руб­лей, то средний доход для этих 10 человек составит 6540 рублей. Эта цифра не позво­ляет судить о всей группе, и в качестве меры центральной тенденции следовало бы из­брать медиану или моду.

ГЛАВА 4. ПЕРВИЧНЫЕ ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ

Меры центральной тенденции чаще всего используются для сравнения групп по уровню выраженности признака. Если исследователь при этом со­мневается, какую меру использовать, то можно дать простые советы.

Выборочные средние можно сравнивать, если выполняются следующие условия:

□ группы достаточно большие, чтобы судить о форме распределения;

□ распределения симметричны;

□ отсутствуют «выбросы».

Если хотя бы одно из перечисленных условий не выполняется, то следует ограничиться модой и медианой. Альтернативой является «сквозное» ранжи­рование представителей сравниваемых групп и сравнение средних, вычис­ленных для рангов этих групп.

КВАНТИЛИ РАСПРЕДЕЛЕНИЯ

Помимо мер центральной тенденции в психологии широко используются меры положения, которые называются квантилями распределения. Кван­тиль — это точка на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на две группы с известным соотно­шением их численности. С одним из квантилей мы уже знакомы — это меди­ана. Это значение признака, которое делит всю совокупность измерений на две группы с равной численностью. Кроме медианы часто используются про-центили и квартили.

Процентили (Percentiles) — это 99 точек — значений признака (Р_и..., Р₉₉), которые делят упорядоченное (по возрастанию) множество наблюдений на 100 частей, равных по численности. Определение конкретного значения про-центиля аналогично определению медианы. Например, при определении 10-го процентиля, Р₁₀, сначала все значения признака упорядочиваются по возрас­танию. Затем отсчитывается 10% испытуемых, имеющих наименьшую выра­женность признака. Р_]а будет соответствовать тому значению признака, кото­рый отделяет эти 10% испытуемых от остальных 90%.

Квартили (Quartiles) — это 3 точки — значения признака (P_2i, P_i0, P₇₅), ко­торые делят упорядоченное (по возрастанию) множество наблюдений на 4 рав­ные по численности части. Первый квартиль соответствует 25-му проценти-лю, второй — 50-му процентилю или медиане, третий квартиль соответствует 75-му процентилю.

Процентили и квартили используются для определения частоты встречае­мости тех или иных значений (или интервалов) измеренного признака или для выделения подгрупп и отдельных испытуемых, наиболее типичных или нетипичных для данного множества наблюдений.

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

МЕРЫ ИЗМЕНЧИВОСТИ

Меры центральной тенденции отражают уровень выраженности измерен­ного признака. Однако не менее важной характеристикой является выражен­ность индивидуальных различий испытуемых по измеренному признаку. Меры изменчивости (Dispersion) применяются в психологии для численного выраже­ния величины межиндивидуальной вариации признака.

Наиболее простой и очевидной мерой изменчивости является размах, ука­зывающий на диапазон изменчивости значений. Размах (Range) — это просто разность максимального и минимального значений:

Ясно, что это очень неустойчивая мера изменчивости, на которую влияют любые возможные «выбросы». Более устойчивыми являются разновидности размаха: размах от 10 до 90-го процентиля (Р₉₀ — Р₁₀) или междуквартильный размах (Р₇₅ — P₂s)- Последние две меры изменчивости находят свое примене­ние для описания вариации в порядковых данных. А для метрических данных используется дисперсия — величина, название которой в науке является си­нонимом изменчивости.

Дисперсия (Variance) — мера изменчивости для метрических данных, про­порциональная сумме квадратов отклонений измеренных значений от их арифметического среднего:

Чем больше изменчивость в данных, тем больше отклонения значений от среднего, тем больше величина дисперсии. Величина дисперсии получается

при усреднении всех квадратов отклонении:

N

N

(4.5)

Следует отличать теоретическую (генеральную) дисперсию — меру измен­чивости бесконечного числа измерений (в генеральной совокупности, попу­ляции в целом) и эмпирическую, или выборочную, дисперсию — для реально измеренного множества значений признака. Выборочное значение в стати­стике используется для оценки дисперсии в генеральной совокупности. Выше указана формула для генеральной (теоретической) дисперсии (D_x), которая, понятно, не вычисляется. Для вычислений используется формула выбороч­ной (эмпирической) дисперсии (D_x), отличающаяся знаменателем:

N-X

(4.6)

ГЛАВА 4. ПЕРВИЧНЫЕ ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ

ПРИМЕР

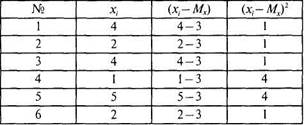
Вычислим дисперсию признакаХдля выборки N= 6:

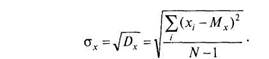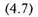На практике чаще используется именно стандартное отклонение, а не дис­персия. Это связано с тем, что сигма выражает изменчивость в исходных еди­ницах измерения признака, а дисперсия — в квадратах исходных единиц.

Свойства дисперсии:

1. Если значения измеренного признака не отличаются друг от друга (рав­
ны между собой) — дисперсия равна нулю. Это соответствует отсутствию из­
менчивости в данных.

2. Прибавление одного и того же числа к каждому значению переменной
не меняет дисперсию:

D_{x + C} = D_x, так как X [(*,■+с) - (М_х+с)]² = Х(х,- - М_х)².

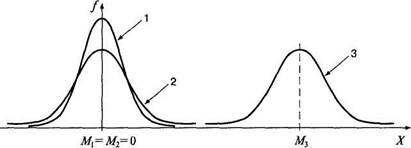
Рис. 4.1. Графики распределения частот: с разной дисперсией (D^Dj), одинаковой дисперсией (D₂= D_}) и разными средними арифметическими (М₂<М₁)

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

Прибавление константы к каждому значению переменной сдвигает график распределения этой переменной на эту константу (меняется среднее), но из­менчивость (дисперсия) при этом остается неизменной.

3. Умножение каждого значения переменной на константу с изменяет дис­персию в с² раз:

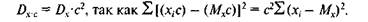
При объединении двух выборок с одинаковой дисперсией, но с разными средними значениями дисперсия увеличивается.

ПРИМЕР______________________________________________________________

Если одна группа содержит значения: 1,1,1,1, 1, а другая группа —значения 3,3, 3, 3, 3, то дисперсии этих групп одинаковы и равны 0. Если же объединить эти две группы, то дисперсия будет равна не 0, а 1.

Вообще говоря, справедливо утверждение: при объединении двух групп к внутригрупповой дисперсии каждой группы добавляется дисперсия, обуслов­ленная различием между группами (их средними). И чем больше различие между средними значениями, тем больше увеличивается дисперсия объеди­ненных групп.

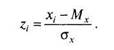Стандартизация или z-преобразование данных — это перевод измерений в стандартную Z-шкалу (Z-scores) со средним M_z = О и D_z (или а_г) = 1. Сначала для переменной, измеренной на выборке, вычисляют среднее М_х стандарт­ное отклонение <з_х. Затем все значения переменной х, пересчитываются по формуле:

(4.8)

В результате преобразованные значения (^-значения) непосредственно выражаются в единицах стандартного отклонения от среднего. Если для од­ной выборки несколько признаков переведены в ^-значения, появляется воз­можность сравнения уровня выраженности разных признаков у того или иного испытуемого. Для того чтобы избавиться от неизбежных отрицательных и дробных значений, можно перейти к любой другой известной шкале: IQ (сред­нее 100, сигма 15); Т-оценок (среднее 50, сигма 10); 10-балльной — стенов (среднее 5,5, сигма 2) и др. Перевод в новую шкалу осуществляется путем умножения каждого г-значения на заданную сигму и прибавления среднего:

(4.9)

Асимметрия (Skewness) — степень отклонения графика распределения час­тот от симметричного вида относительно среднего значения. Если исходные данные переведены в ^-значения, показатель асимметрии вычисляется по формуле:

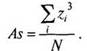As = -

N

(4.10)

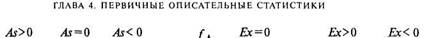X X

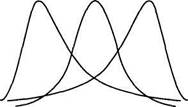
Рис. 4.2. Распределения частот с разными значениями асимметрии и эксцесса

Для симметричного распределения асимметрия равна 0. Если чаще встре­чаются значения меньше среднего, то говорят о левосторонней, или положи­тельной асимметрии (As > 0). Если же чаще встречаются значения больше сред­него, то асимметрия — правосторонняя, или отрицательная (As<0). Чем больше отклонение от нуля, тем больше асимметрия.

Эксцесс (Kurtosis) — мера плосковершинности или остроконечности гра­фика распределения измеренного признака. Если исходные данные переве­дены в ^-значения, показатель эксцесса определяется формулой:

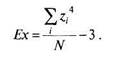(4.11)

Островершинное распределение характеризуется положительным эксцес­сом (Ех > 0), а плосковершинное — отрицательным (-3 < Ех < 0). «Средневер-шинное» (нормальное) распределение имеет нулевой эксцесс (Ех = 0).

Задачи и упражнения

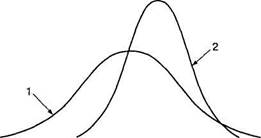
1. По результатам измерения общительности у юношей (1) и девушек (2)
были построены сглаженные графики распределения частот (рис. 4.3).

2. Определите по графику: а) как различаются средние М_х и М₂; б) как раз­
личаются дисперсии D_{ и /)₂?

3. Вычислите дисперсии для двух групп:

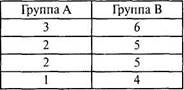
Какой будет дисперсия 8 значений, полученных путем объединения групп? Объясните полученный результат.

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

Л

Общительность

Рис. 4.3. Графики распределения относительных частот общительности юношей (1) и девушек (2)

ОБРАБОТКА НА КОМПЬЮТЕРЕ

Способ 1. Выбираем Analyze > Descriptive Statistics > Frequencies... В открыв­шемся диалоговом окне (Frequencies) переносим из левой в правую часть ин­тересующие нас переменные. Если таблица распределения частот нас не ин­тересует, снимаем флажок Display frequency tables (Показывать таблицы частот). Нажимаем кнопку Statistics... Выбираем интересующие нас статистики и от­мечаем их флажком: центральной тенденции (Central Tendency) — среднее (Mean), моду (Mode), медиану (Median); изменчивости (Dispersion) — стан­дартное отклонение (Std. deviation), дисперсию (Variance); распределения — асимметрию (Skewness) и эксцесс (Kurtosis). После этого нажимаем Continue, затем ОК и получаем результат.

Способ 2. Выбираем Analyze > Descriptive Statistics > Descriptives... В от­крывшемся диалоговом окне переносим из левой в правую часть интересую­щие нас переменные. Нажимаем кнопку Options... и отмечаем флажком те статистики, которые нас интересуют (см. выше). Нажимаем Continue, затем ОК и получаем результат.

Глава 5