ПРИМЕРЫ

1. Значение IQ по шкале Векслера (Л/= 100; а = 15) некоторого тестируемого рав­но 125. Вопрос о степени выраженности интеллекта у данного индивидуума пе­реформулируем следующим образом: насколько часто или редко встречаются зна­чения IQ ниже или выше 125? Решение. Перейдем от шкалы IQ к единицам

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

стандартного отклонения (г-значениям): г=(125-100)/15= 1,66. По таблице из приложения 1 находим площадь под кривой справа от этого значения, она рав­на 0,0485. Это значит, что IQ 125 и выше встречается довольно редко — менее, чем в 5% случаев.

2. Какова вероятность того, что случайно выбранный человек будет иметь 1Q по шкале Векслера в диапазоне от 100 до 120? Решение. В единицах стандартного отклонения Zi =0,0; Zi ⁼ 1,66. Площадь справа от Z\ —0,5, справа от Zj — пример­но 0,0918, следовательно, площадь между Z\ и г₂ равна 0,5-0,0918 = 0,4082. Та­ким образом, вероятность того, что случайно выбранный человек будет иметь IQ в диапазоне от 100 до 120, равна примерно 0,41.

Несмотря на исходный постулат, в соответствии с которым свойства в ге­неральной совокупности имеют нормальное распределение, реальные дан­ные, полученные на выборке, нечасто распределены нормально. Более того, разработано множество методов, позволяющих анализировать данные без всякого предположения о характере их распределения как в выборке, так и в генеральной совокупности. Эти обстоятельства иногда приводят к ложному убеждению, что нормальное распределение — пустая математическая аб­стракция, не имеющая отношения к психологии. Тем не менее, как мы уви­дим в дальнейшем, можно указать по крайней мере на три важных аспекта применения нормального распределения:

1. Разработка тестовых шкал.

2. Проверка нормальности выборочного распределения для принятия ре­
шения о том, в какой шкале измерен признак — в метрической или по­
рядковой.

3. Статистическая проверка гипотез, в частности — при определении риска
принятия неверного решения.

РАЗРАБОТКА ТЕСТОВЫХ ШКАЛ

Тестовые шкалы разрабатываются для того, чтобы оценить индивидуаль­ный результат тестирования путем сопоставления его с тестовыми нормами, полученными на выборке стандартизации. Выборка стандартизации специаль­но формируется для разработки тестовой шкалы — она должна быть репре­зентативна генеральной совокупности, для которой планируется применять данный тест. Впоследствии при тестировании предполагается, что и тестиру­емый, и выборка стандартизации принадлежат одной и той же генеральной совокупности.

Исходным принципом при разработке тестовой шкалы является предпо­ложение о том, что измеряемое свойство распределено в генеральной сово­купности в соответствии с нормальным законом. Соответственно, измерение в тестовой шкале данного свойства на выборке стандартизации также должно обеспечивать нормальное распределение. Если это так, то тестовая шкала яв-

ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

ляется метрической — точнее, равных интервалов. Если это не так, то свой­ство удалось отразить в лучшем случае — в шкале порядка. Естественно, что большинство стандартных тестовых шкал являются метрическими, что по­зволяет более детально интерпретировать результаты тестирования — с уче­том свойств нормального распределения — и корректно применять любые методы статистического анализа. Таким образом, основная проблема стандар­тизации теста заключается в разработке такой шкалы, в которой распределе­ние тестовых показателей на выборке стандартизации соответствовало бы нормальному распределению.

Исходные тестовые оценки — это количество ответов на те или иные воп­росы теста, время или количество решенных задач и т. д. Они еще называют­ся первичными, или «сырыми» оценками. Итогом стандартизации являются тестовые нормы — таблица пересчета «сырых» оценок в стандартные тестовые шкалы.

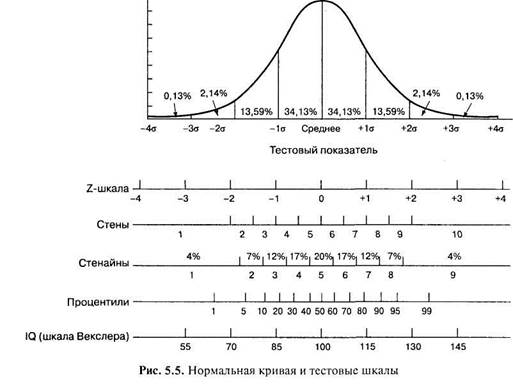Существует множество стандартных тестовых шкал, основное назначение которых — представление индивидуальных результатов тестирования в удоб­ном для интерпретации виде. Некоторые из этих шкал представлены на рис. 5.5. Общим для них является соответствие нормальному распределению, а различаются они только двумя показателями: средним значением и мас­штабом (стандартным отклонением — о), определяющим дробность шкалы.

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

Общая последовательность стандартизации (разработки тестовых норм — таб­лицы пересчета «сырых» оценок в стандартные тестовые) состоит в следующем:

1) определяется генеральная совокупность, для которой разрабатывается
методика и формируется репрезентативная выборка стандартизации;

2) по результатам применения первичного варианта теста строится рас­
пределение «сырых» оценок;

3) проверяют соответствие полученного распределения нормальному за­
кону;

4) если распределение «сырых» оценок соответствует нормальному, про­
изводится линейная стандартизация;

5) если распределение «сырых» оценок не соответствует нормальному, то
возможны два варианта:

• перед линейной стандартизацией производят эмпирическую норма­
лизацию;

• проводят нелинейную нормализацию.

Проверка распределения «сырых» оценок на соответствие нормальному закону производится при помощи специальных критериев, которые мы рас­смотрим далее в этой главе.

Линейная стандартизация заключается в том, что определяются границы интервалов «сырых» оценок, соответствующие стандартным тестовым пока­зателям. Эти границы вычисляются путем прибавления к среднему «сырых» оценок (или вычитания из него) долей стандартных отклонений, соответству­ющих тестовой шкале. Пример, приведенный ниже, демонстрирует процеду­ру линейной стандартизации.

ПРИМЕР_______________________________________________________________

Предположим, получено распределение «сырых» оценок, соответствующее нор­мальному, со средним М_х = 22 и стандартным отклонением о_х= 6. В качестве стан­дартной тестовой шкалы выбрана 10-балльная шкала стенов, предложенная Р. Кет-телом {M_st = 5,5; o_sl = 2). Результатом линейной стандартизации должна являться таблица пересчета из шкалы «сырых» оценок в шкалу стенов. Для этого каждому стандартному значению ставится в соответствие интервал «сырых» оценок. Грани­цы интервалов определяются следующим образом. Среднее «сырых» оценок долж­но делить шкалу стенов ровно пополам (1—5 — ниже среднего, 6—10 — выше сред­него). Следовательно, среднее «сырых» оценок М_х = 22 — это граница стенов 5 и 6. Следующая граница справа — отделяющая стены 6 и 7 — отстоит от среднего на a_s,/2. Этой границе должна соответствовать граница «сырых» оценок М_х + о_х/2 = 22 + 3 = 25. Так же определяются границы всех оставшихся интервалов, а границы крайних интервалов остаются открытыми. Результатом являются тестовые нормы — таблица пересчета «сырых» баллов в стандартные тестовые оценки (табл. 5.1)¹.

¹ Обратите внимание, что левая граница каждого диапазона «сырых» оценок исключает гра­ницу интервалов, а правая — включает ее. Можно было бы сделать и наоборот, но главное, чтобы границы соседних диапазонов не совпадали, во избежание недоразумений при попада­нии индивидуального значения на границу интервалов.

ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

Табл ица 5.1 Тестовые нормы — таблица пересчета «сырых» баллов в стены

Стены
«Сырые» баллы	<11	11-13	14-16	17-19	20-22	23-25	26-28	29-31	32-34	>34

Пользуясь этой таблицей тестовых норм индивидуальный результат («сырой» балл) переводят в шкалу стенов, что позволяет интерпретировать выраженность измеря­емого свойства.

В общем случае границы интервалов определяются по формуле г-преоб-разования:

K/f с/.— A/f /т

о\

z = -

о\

где Xj — искомая граница интервала «сырых» оценок, st_t — граница интервала в стандартной тестовой шкале, М_х, о_х, M_sh o_sl — средние и стандартные откло­нения «сырых» оценок (х) и стандартной шкалы (st).

Эмпирическая нормализация применяется, когда распределение «сырых» баллов отличается от нормального. Она заключается в изменении содер­жания тестовых заданий. Например, если «сырая» оценка — это количе­ство задач, решенных испытуемыми за отведенное время, и получено рас­пределение с правосторонней асимметрией, то это значит, что слишком большая доля испытуемых решает больше половины заданий. В этом случае необходимо либо добавить более трудные задания, либо сократить время решения.

Нелинейная нормализация применяется, если эмпирическая нормализа­ция невозможна или нежелательна, например, с точки зрения затрат вре­мени и ресурсов. В этом случае перевод «сырых» оценок в стандартные про­изводится через нахождение процентильных границ групп в исходном распределении, соответствующих процентильным границам групп в нор­мальном распределении стандартной шкалы. Каждому интервалу стандарт­ной шкалы ставится в соответствие такой интервал шкалы «сырых» оценок, который содержит ту же процентную долю выборки стандартизации. Вели­чины долей определяются по площади под единичной нормальной кривой, заключенной между соответствующими данному интервалу стандартной шкалы г-оценками.

Например, для того чтобы определить, какой «сырой» балл должен соот­ветствовать нижней границе стена 10, необходимо сначала выяснить, какому г-значению соответствует эта граница (z = 2). Затем по таблице нормального распределения (приложение 1) надо определить, какая доля площади под нормальной кривой находится правее этого значения (0,023). После этого определяется, какое значение отсекает 2,3% наибольших значений «сырых» баллов выборки стандартизации. Найденное значение и будет соответство­вать границе 9 и 10 стена.

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

ПРИМЕР

Рассмотрим пример нелинейной нормализации. Допустим, разрабатываемый тест предполагает решение 20 заданий. Объем выборки стандартизации N= 200 чело­век. Сначала строится таблица распределения частот «сырых» оценок (табл. 5.2).

Таб л и ца 5.2

Таблица распределения частот

«сырыхх

» оценок

Оценка

Частота

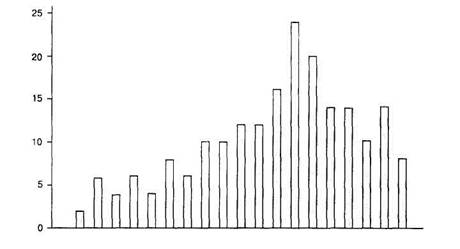
Исходное распределение заметно отличается от нормального — оно имеет право­стороннюю асимметрию (рис. 5.6). В качестве стандартной выберем шкалу стенай-нов, для каждой градации которой известны процентные доли (см. рис. 5.5). Исхо­дя из этих процентных долей и таблицы распределения «сырых» оценок строится таблица тестовых норм (табл. 5.3). Сначала отбираются 4% испытуемых, решив­ших наименьшее количество заданий. У нас 8 испытуемых (4%) решили менее 4 за­даний. Это число заданий будет соответствовать 1 -му стенайну. Второму стенайну будет соответствовать результат следующих 7% (14) испытуемых: от 4 до 6 заданий, и т. д. Итог нелинейной стандартизации — таблица перевода «сырых» оценок в шкальные, стенайны (табл. 5.3).

Табл и ца 5.3 Пример нелинейной нормализации: пересчет «сырых» оценок в шкалу стенайнов

Стенайны
%
«Сырые» оценки	<4	4-6	7-9	10-12	13-14	15-16	17-18

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Рис. 5.6. Распределение «сырых» оценок (по данным табл. 5.2)

Изложенные основы психодиагностики позволяют сформулировать мате­матически обоснованные требования к тесту. Тестовая методика должна со­держать:

ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

□ описание выборки стандартизации;

□ характеристику распределения «сырых» баллов с указанием среднего и
стандартного отклонения;

□ наименование, характеристику стандартной шкалы;

□ тестовые нормы — таблицы пересчета «сырых» баллов в шкальные.

ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ

Для проверки нормальности используются различные процедуры, позво­ляющие выяснить, отличается ли от нормального выборочное распределение измеренной переменной. Необходимость такого сопоставления возникает, когда мы сомневаемся в том, в какой шкале представлен признак — в поряд­ковой или метрической. А сомнения такие возникают очень часто, так как заранее нам, как правило, не известно, в какой шкале удастся измерить изу­чаемое свойство (исключая, конечно, случаи явно номинативного измерения).

Важность определения того, в какой шкале измерен признак, трудно пе­реоценить, по крайней мере, по двум причинам. От этого зависит, во-первых, полнота учета исходной эмпирической информации (в частности, об инди­видуальных различиях), во-вторых, доступность многих методов анализа дан­ных. Если исследователь принимает решение об измерении в порядковой шкале, то неизбежное последующее ранжирование ведет к потере части ис­ходной информации о различиях между испытуемыми, изучаемыми группа­ми, о взаимосвязях между признаками и т. д. Кроме того, метрические дан­ные позволяют использовать значительно более широкий набор методов анализа и, как следствие, сделать выводы исследования более глубокими и содержательными.

Наиболее весомым аргументом в пользу того, что признак измерен в мет­рической шкале, является соответствие выборочного распределения нормаль­ному. Это является следствием закона нормального распределения. Если вы­борочное распределение не отличается от нормального, то это значит, что измеряемое свойство удалось отразить в метрической шкале (обычно — интер­вальной).

Существует множество различных способов проверки нормальности, из которых мы кратко опишем лишь некоторые, предполагая, что эти проверки читатель будет производить при помощи компьютерных программ.

Графический способ (Q-Q Plots, Р-Р Plots). Строят либо квантильные гра­фики, либо графики накопленных частот. Квантильные графики (Q-Q Plots) строятся следующим образом. Сначала определяются эмпирические значе­ния изучаемого признака, соответствующие 5, 10,..., 95-процентилю. Затем по таблице нормального распределения для каждого из этих процентилей определяются z-значения (теоретические). Два полученных ряда чисел за­дают координаты точек на графике: эмпирические значения признака от-

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

кладываются на оси абсцисс, а соответствующие им теоретические значе­ния — на оси ординат. Для нормального распределения все точки будут ле­жать на одной прямой или рядом с ней. Чем больше расстояние от точек до прямой линии, тем меньше распределение соответствует нормальному. Гра­фики накопленных частот (Р-Р Plots) строятся подобным образом. На оси абсцисс через равные интервалы откладываются значения накопленных от­носительных частот, например 0,05; 0,1;...; 0,95. Далее определяются эмпи­рические значения изучаемого признака, соответствующие каждому значе­нию накопленной частоты, которые пересчитываются в z-значения. По таблице нормального распределения определяются теоретические накоп­ленные частоты (площадь под кривой) для каждого из вычисленных г-зна-чений, которые откладываются на оси ординат. Если распределение со­ответствует нормальному, полученные на графике точки лежат на одной прямой.

Критерии асимметрии и эксцесса. Эти критерии определяют допустимую степень отклонения эмпирических значений асимметрии и эксцесса от нуле­вых значений, соответствующих нормальному распределению. Допустимая степень отклонения — та, которая позволяет считать, что эти статистики су­щественно не отличаются от нормальных параметров. Величина допустимых отклонений определяется так называемыми стандартными ошибками асим­метрии и эксцесса. Для формулы асимметрии (4.10) стандартная ошибка оп­ределяются по формуле:

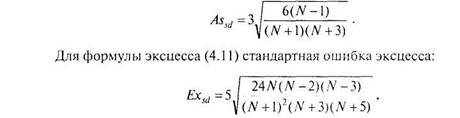где N — объем выборки.

Выборочные значения асимметрии и эксцесса значительно отличаются от нуля, если не превышают значения своих стандартных ошибок. Это можно считать признаком соответствия выборочного распределения нормальному закону. Следует отметить, что компьютерные программы вычисляют показа­тели асимметрии, эксцесса и соответствующие им стандартные ошибки по другим, более сложным формулам.

Статистический критерий нормальности Колмогорова-Смирнова считается наиболее состоятельным для определения степени соответствия эмпиричес­кого распределения нормальному. Он позволяет оценить вероятность того, что данная выборка принадлежит генеральной совокупности с нормальным распределением. Если эта вероятность р< 0,05, то данное эмпирическое распределение существенно отличается от нормального, а если р > 0,05, то делают вывод о приблизительном соответствии данного эмпирического рас­пределения нормальному.

ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

Причины отклонения от нормальности. Общей причиной отклонения фор­мы выборочного распределения признака от нормального вида чаще всего является особенность процедуры измерения: используемая шкала может об­ладать неравномерной чувствительностью к измеряемому свойству в разных частях диапазона его изменчивости.

ПРИМЕР

Предположим, выраженность некоторой способности определяется количеством выполненных заданий за отведенное время. Если задания простые или время слиш­ком велико, то данная измерительная процедура будет обладать достаточной чув­ствительностью лишь в отношении части испытуемых, для которых эти задания достаточно трудны. И слишком большая доля испытуемых будет решать все или почти все задания. В итоге мы получим распределение с выраженной правосторон­ней асимметрией. Можно, конечно, впоследствии повысить качество измерения путем эмпирической нормализации, добавив более сложные задания или сократив время выполнения данного набора заданий. Если же мы чрезмерно усложним из­мерительную процедуру, то возникнет обратная ситуация, когда большая часть ис­пытуемых будет решать малое количество заданий и эмпирическое распределение приобретет левостороннюю асимметрию.

Таким образом, такие отклонения от нормального вида, как право- или левосторонняя асимметрия или слишком большой эксцесс (больше 0), связа­ны с относительно низкой чувствительностью измерительной процедуры в области моды (вершины графика распределения частот).

Последствия отклонения от нормальности. Следует отметить, что задача получения эмпирического распределения, строго соответствующего нормаль­ному закону, нечасто встречается в практике исследования. Обычно такие случаи ограничиваются разработкой новой измерительной процедуры или тестовой шкалы, когда применяется эмпирическая или нелинейная норма­лизация для «исправления» эмпирического распределения. В большинстве случаев соответствие или несоответствие нормальности является тем свой­ством измеренного признака, который исследователь должен учитывать при выборе статистических процедур анализа данных.

Заметно ли "на глаз" отличие распределения от нормального вида?

X

В общем случае при значительном отклонении эмпирического распреде­ления от нормального следует отказаться от предположения о том, что при­знак измерен в метрической шкале. Но остается открытым вопрос о том, како­ва мера существенности этого отклоне­ния? Кроме того, разные методы ана­лиза данных обладают различной чувствительностью к отклонениям от нормальности. Обычно при обоснова­нии перспективности этой проблемы приводят принцип Р. Фишера, одного из «отцов-основателей» современной статистики: «Отклонения от нормально-

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

го вида, если только они не слишком заметны, можно обнаружить лишь для боль­ших выборок; сами по себе они вносят малое отличие в статистические крите­рии и другие вопросы»¹. К примеру, при малых, но обычных для психологичес­ких исследований выборках (до 50 человек) критерий Колмогорова-Смирнова недостаточно чувствителен при определении даже весьма заметных «на глаз» отклонений от нормальности. В то же время некоторые процедуры анализа метрических данных вполне допускают отклонения от нормального распре­деления (одни — в большей степени, другие — в меньшей). В дальнейшем при изложении материала мы при необходимости будем оговаривать меру жесткости требования нормальности.

Задачи и упражнения

1. Некоторое свойство измеряется при помощи тестовой шкалы СЕЕВ
(Л/=500, о= 100). Какая приблизительно доля генеральной совокупно­
сти имеет балл от 600 до 700?

2. В генеральной совокупности значения IQ в шкале Векслера распределе­
ны приблизительно нормально со средним 100 и стандартным отклоне­
нием 15. С помощью таблиц определите следующие вероятности:

а) вероятность того, что случайно выбранный человек будет иметь IQ
между 79 и 121;

б) вероятность того, что случайно выбранный человек будет иметь IQ
выше 127; ниже 73.

3. Определите при помощи квантильного графика, соответствует ли нор­
мальному виду распределение переменной со следующими значениями
процентилей:

В области каких значений шкала, в которой измерен признак, обладает большей дифференцирующей способностью (чувствительностью), а в какой — меньшей?

ОБРАБОТКА НА КОМПЬЮТЕРЕ

Критерии асимметрии и эксцесса. Выбираем Analyze > Descriptive Statistics > Descriptives... В окне диалога переносим из левого окна в правое интересующие нас переменные. Нажимаем кнопку Options..., ставим флажок Distribution >

¹ Цит. по: Справочник по прикладной статистике: В 2 т. / Под ред. Э. Ллойда, У. Ледермана. М., 1989. Т. 1.С. 270.

ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

Kurtosis, Skewness, нажимаем Continue, затем ОК. В таблице результатов стол­бцы Kurtosis и Skewness содержат значения асимметрии (Kurtosis) и эксцесса (Skewness) и соответствующие им стандартные ошибки (Std. Error). Распреде­ление соответствует нормальному виду, если для соответствующей переменной абсолютные значения асимметрии и эксцесса не превышают свои стандартные ошибки.

Графический способ. Выбираем Graphs > РР... — графики накопленных ча­стот (или Graphs > QQ... — квантильные графики). Открывается диалог Р-Р Plots (Q-Q Plots). Переносим из левого в правое окно интересующие нас пе­ременные. Нажимаем ОК. В окне результатов просматриваем графики Normal Р-Р Plot... (Normal Q-Q Plot...), на которых по горизонтальной оси отложены соответствующие эмпирические значения, а по вертикальной оси — теорети­ческие значения. Чем ближе точки графиков к прямой линии, тем меньше от­личие распределения от нормального вида.

Критерий нормальности Колмогорова-Смирнова. Выбираем Analyze > Nonpa-rametric Tests > 1-Sample K-S... Открывается диалог One-Sample Kolmogorov-Smirnov Test. Переносим из левого в правое окно интересующие нас пере­менные. Нажимаем ОК. В соответствующем переменной столбце находим Kolmogorov-SmirnovZ (значение критерия) и Asymp. Sig. (2-tailed) (вероятность того, что распределение соответствует нормальному виду). Если значение Asymp. Sig. меньше или равно 0,05, то распределение существенно отличает­ся от нормального вида. Если Asymp. Sig. больше 0,05, то существенного от­личия от нормальности не обнаружено.

Глава 6