Еще раз про расстановку сил

Автор: – Вернёмся к проблеме расстановки сил. Рассмотрим шарик, подвешенный на ниточке в двух случаях рис.2.5.1: а) шарик совершает колебания, б) шарик равномерно вращается по окружности в горизонтальной плоскости. Как мы понимаем, на тело действуют только две силы – тяжести и реакции нити. А движения отличаются. Почему?

Студент: – Все дело в начальных условиях. Как мы уже неоднократно видели, направления силы и скорости могут не совпадать.

Автор: – Можно отметить, что в данных примерах совокупность сил действительно одинаковая, но числовые соотношения между действующими силами при этом различны. Это означает, что равнодействующие силы тоже различаются. Так, при равномерном движении по окружности равнодействующая сила направлена к центру, тогда как при колебаниях равнодействующая меняет свой угол по отношению к нити и является возвращающей силой. Отсюда следует, что данные о характере движения частицы и не должны служить отправной точкой при определении сил, но они не лишние. Для тренировки определите, пожалуйста, силы натяжения Т ₁и Т ₂ в примерах а) и б) соответственно.

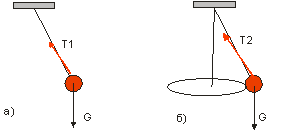
Рис.2.5.1

Студент: – Предположим, что известен угол α между вертикалью и нитью.

Рис.2.5.2

В случае а) разложим вектор силы тяжести по направлению равнодействующей и перпендикулярно ей (т. е. вдоль нити). Приравняем силы, перпендикулярные смещению, получаем:

Т = G cosα= mg cosα.

Автор: – Здесь Вы допустили досадную ошибку, характерную для многих студентов. Дело в том, что во втором законе Ньютона есть «невинная» фраза, про которую забывают. Этот закон справедлив только для инерциальных систем отсчета. А Вы стали проецировать силы на ось, совпадающую с ниткой. Это, как видно, ось координат, движущаяся с ускорением. Поэтому второй закон Ньютона здесь не выполняется. Надо поступить по-другому. Раз тело совершает движение по окружности, то центростремительная сила будет равна проекции равнодействующей всех сил на радиус-вектор.

Т– Gcosα=mV²/R; Т= mV²/R +mgcosα.

Здесь R – радиус вращения, что совпадает с длиной нити. Таким образом, сила Т зависит от скорости тела в данной точке. Для ответа на поставленный вопрос нам необходимо знать, с какой высоты это тело начало свое путешествие.

Студент: – Во втором случае равнодействующая есть центростремительная сила и направлена по горизонтали. Поэтому удобно разложить силу Т на вертикальное и горизонтальное направления. Приравняем проекции сил на вертикаль (смещения по вертикали нет, и мы работаем в лабораторной системе отсчета, которая является инерциальной).

Т cosα= mg, или Т = mg/ cosα.

Автор: – Вы получили силу реакции нити. Искомая сила натяжения равна ей по модулю и направлена в противоположную сторону. Во многих задачах, правда, для них используют одно название, подразумевая при этом абсолютное значение силы.

Студент: – Если я правильно понял, то, зная взаимодействие тел, можно выявить силы, приложенные к нему. А определив эти силы и начальные условия, можно предсказать характер движения частицы.

Автор: – Вы правильно рассуждаете.

В заключение, в качестве философского отступления и вместо традиционной истории, а также для тренировки мышления, хочу предложить Вам знаменитый парадокс движения, который называется "Собака Остина". Придумал его английский математик А. К. Остин.

Из одной точки по прямой дороге одновременно отправились в путь девочка, мальчик и собачка. Мальчик и девочка двигаются в одном направлении – мальчик со скоростью 7 км/ч, девочка со скоростью 5 км/ч, а собачка бегает между ними со скоростью 10 км/ч. Причем, добежав до одного из ребят, она, лизнув его, разворачивается и бежит обратно. Где будет находиться собачка через 1 час этого путешествия, и в какую сторону она побежит?

Оказывается, можно обосновать, что собачка может находиться в любой точке между мальчиком и девочкой и бежать в любую сторону.

Студент: –?..

Автор: – Правдоподобное решение выглядит так. Через 1 час мальчик пройдет 7 км, а девочка – 5 км. Поместив собачку в произвольную точку и развернув ей мордочку в любом направлении, обратим во времени движение. Тогда через час все наши участники движения встретятся в начальной точке. Другими словами, если бы мы неоднократно осуществляли ситуацию, описанную в задаче, то собачка каждый раз могла бы оказываться в новой конечной точке, хотя начальные стартовые условия были одинаковы.

Парадокс "обнажается" при анализе начала движения. Действительно, простой вопрос – может ли собачка начать движение, строго соблюдая все условия задачи? Нет ответа. Ведь уже в первый момент ей придется сделать бесконечно много поворотов. Физически это неосуществимо. А раз вектор начальной скорости не определен, то и нет однозначности в конечном положении собачки.

Студент: – Эта неоднозначность хитро "замаскировалась" в условии задачи.

Автор: – Разберем несложную задачу на второй закон Ньютона.

Задача 2.1. Два тела, массы которых М и m (М > m), подняли на одинаковую высоту и одновременно отпустили. Сила сопротивления воздуха для них одинаковая и постоянная. Какое тело упадет раньше?

Студент: – Поскольку сила сопротивления воздуха для обоих тел одинакова, то ее можно не принимать во внимание. Значит, оба тела упадут одновременно.

Автор: – Очень странные рассуждения. Вы опять рассуждали произвольно, не основываясь на законах Ньютона. Давайте, как всегда, разбираться последовательно. Какие силы действуют на тела?

Студент: – В задаче фигурируют две силы: тяжести Мg и сопротивления F. Равнодействующая этих сил Мg– F (для тяжелого тела).

Автор: – Как отсюда найти ускорение?

Студент: – По второму закону Ньютона а = (Мg– F)/М, или

а = g– F/М. Соответственно, для легкого тела имеем а₁ =g– F /m; а > а₁. Значит, быстрее упадет тяжелое тело.

Автор: – Рассмотрим известный пример-парадокс на третий закон Ньютона.

Лошадь тянет сани, и оба они двигаются с некоторым ускорением. Однако из третьего закона Ньютона следует, что с какой силой лошадь тянет сани, с такой же силой, но в обратную сторону, сани действуют на лошадь. Почему же эта система все-таки двигается ускоренно?

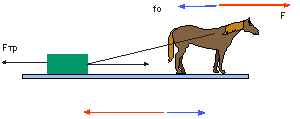
Рис.2.5.3

Студент: – Я никогда не задумывался над этим вопросом. Но не вижу здесь особых трудностей. Силы, о которых Вы говорили, не могут взаимно уничтожаться, т. к. приложены к разным телам: одна к лошади, другая к саням.

Автор: – Но ведь они связаны и образуют одну систему. Согласно третьему закону Ньютона, взаимодействие лошади и саней не может привести к движению системы как целого. Значит, в задаче должно участвовать еще одно тело. Таковым является Земля. В результате имеется уже не одно, а целых три взаимодействия: 1) лошади и саней (сила f ₀), 2) лошади и Земли (сила F, сила тяжести здесь не изображена, т.к. она компенсируется силой реакции опоры), 3) саней и Земли (сила F _тр, силы реакции опоры и тяжести также не изображены). Таким образом, к каждому телу приложено по две силы. Равнодействующая сил, приложенных к системе лошадь – сани равна

F _рав =F – F _тр.

Она и вызывает ускорение системы.

Студент: – Получается, что земная поверхность является не просто местом, на котором разыгрываются столь драматические события, но и активным их участником.

Автор: – Действительно, если поставить лошадь с телегой на идеальный лед, исключив горизонтальный контакт с Землей, то лошадь не двинется с места. Никакие внутренние взаимодействия не могут сообщить ускорение системе как целому. Для этого обязательно необходимы воздействия извне. Это есть следствие третьего закона Ньютона.