Задача 1. Уравнение движения точки по прямой имеет вид х = А + Вt + + Сt2, где А = 5 м; В = 4 м/с; с = -1 м/с2. 1) Определить момент времени, в который скорость точки равна u = 0. 2) Найти координату и ускорение в этот момент времени. 3) Определить среднюю скорость за 4 секунды. 4) Построить графики координаты, пути, скорости и ускорения этого движения.
 | Решение. Из уравнения движения х = А + Вt + сt2 найдем скорость: 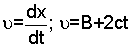 (1.12) и ускорение: (1.12) и ускорение: 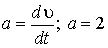 с (1.13) с (1.13) |
1. Определим момент времени t2, в который скорость равна нулю: u = 0, подставив значение скорости в уравнение (1) получим:
0 = В + 2сt, 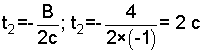
Проверим размерность:
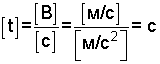 .
.
2. Координата в этот момент времени
х = 5+4.2 + (-1).22 = 9 м.
Проверим размерность
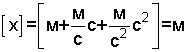 .
.
Ускорение 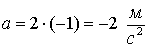 .
.
Проверим размерность 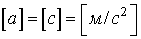 .
.
3. Для определения средней скорости определим координату в моменты времени: t0=0, t2 = 2 с и t1 = 4 с, соответственно:
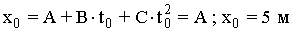 ;
;
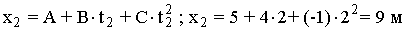 ;
;
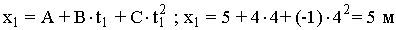 .
.
Пройденный путь за 4 секунды равен: 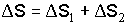 , где путь, пройденный за первые две секунды:
, где путь, пройденный за первые две секунды: 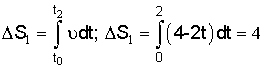 м; путь, пройденный за последние две секунды:
м; путь, пройденный за последние две секунды: 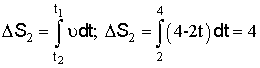 м;
м;
DS = 4 + 4 = 8 м;
DS = (х2 – х0) + (х2 – х1) = (9-5) + (9-5) = 8 м.
Средняя скорость определяется уравнением (1.4):
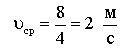 .
.
4. Для построения графиков составим таблицу значений координаты, скорости и ускорения.
| t,с | |||
| х,м | |||
| u, м/с | -4 | ||
| а, м/с2 | -2 | -2 | -2 |
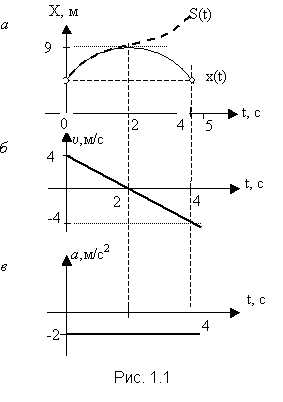 | Определим значения скорости в момент времени t0 =0 и t1 =4 из уравнения (1.1 а) u0 = В; u0 = 4 (м/с); u1 = В + 2сt; u1 = 4 +2.(-1). 4 = -4 м/с. Используя данные таблицы, чертим график координаты (рис. 1.1, а). График пути строим, исходя из следующих соображений: 1) путь и координата до момента времени t2 = 2 c, в которой изменяется знак скорости (ее направление), совпадают; 2) после момента t2 = 2 c координата убывает, а путь продолжает возрастать по тому же закону, по которому убывает координата. График пути до момента времени t2 = 2 c совпадает с графиком координаты, но, начиная с этого момента, является зеркальным отображением графика координаты рис. 1.1, а, штриховая линия. График скорости изображен на рис. 1.1 б, график ускорения – на рис. 1.1, в. |
Ответ: t = 2 с; х = 9 м; а = -2 м/с2; uср = 2,25 м/с.
Задача 2. Автомобиль проходит последовательно два одинаковых участка пути каждый по S = 10 м с постоянным ускорением, причем первый участок пути пройден автомобилем за t1 = 1,5 секунды, а второй – за t2 = 2 секунды. 1) С каким ускорением a движется автомобиль? 2) Какова скорость u0 автомобиля в начале первого участка? 3) Какова скорость u2 в конце второго участка пути?
 | Решение. Для определения ускорения запишем уравнение пути для первого и второго участков: 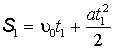 (1.14) (1.14) 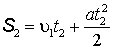 (1.15) (1.15) |
Определим из уравнения (1.2а) начальную скорость: 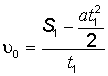 , скорость в начале второго участка:
, скорость в начале второго участка: 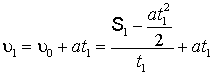 ; подставим полученные выражения в уравнение (1.15):
; подставим полученные выражения в уравнение (1.15):
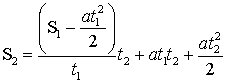 ,
,
решаем уравнение и получаем значение ускорения:
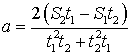 .
.
Проверяем размерность:
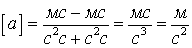 .
.
Произведем расчет
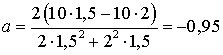 м/с2,
м/с2,
отрицательное значение ускорения означает, что движение равнозамедленное.
2. Определим скорость автомобиля в начале первого участка:
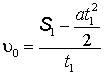 .
.
Проверим размерность:
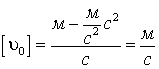 ;
;
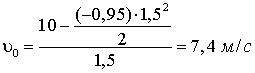 .
.
3. Скорость в конце второго участка
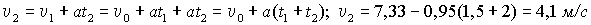 .
.
Размерность
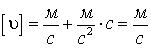 .
.
Ответ: а = -0,95 м/с2; u0 =7,4 м/с; u2 =4,1 м/с.
Задача 3. С некоторой высоты свободно падает тело (рис. 1.2). Через 2 секунды с той же высоты падает второе тело. 1) Через сколько секунд удвоится расстояние, разделяющее тела до начала падения второго тела? 2) Чему равно это расстояние?
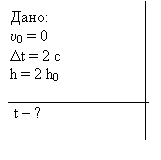 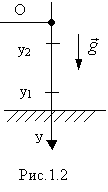 | Решение. Выберем положительное направление оси ОУ по направлению движения (падения) тела. За начало отсчета возьмем начальное положение тела (рис. 1.2). Уравнение движения первого тела 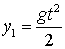 (1) второго (1) второго 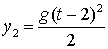 (2) Определим расстояние между телами: (2) Определим расстояние между телами: 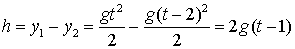 . . |
Для момента времени t = 0 это расстояние h0 = у1-у2 = 2g. Определим время, за которое это расстояние удвоится: h=у1-у2 = 2g(t-1), так как h = 2 h0, то 2 ´ 2g = 2g(t-1). Решая уравнение, получим: t = 6g/2g; t =3 с.
Расстояние между точками в момент времени t:
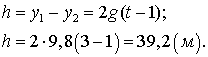
Ответ: t = 3 с, 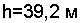 .
.
 2015-10-16
2015-10-16 3032
3032








