Пример 2.3 Условия равновесия произвольной плоской системы сил

Найти моменты относительно точек А и В.

В точке А приложена пара сил с моментом m=6 кНм. (рис. 15).

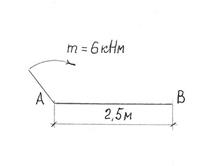
рис. 15

М_А=m=6 кНм

М_В=m=6 кНм

Запомни!

Пара сил "m" на оси не проецируется, на плечо не умножается, в уравнение моментов
относительно любой точки всегда входит с ее знаком.

Пример 2.4

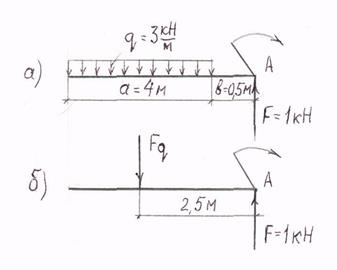
Найти алгебраическую сумму моментов сил относительно точки А. Схема нагружения балки на рис. 16-а. Дано: m = 5 кНм; F = 1 кН; q = 3 кН/м

рис. 16

Рисуем расчетную схему балки (рис. 16-б).

F_q= q ^. a= 3 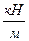^. 4 м = 12 кН

М_А= –F_q^. 2,5+m = –12 ^. 2,5+5 = –25 кНм

Проверь себя

Пример 2.5

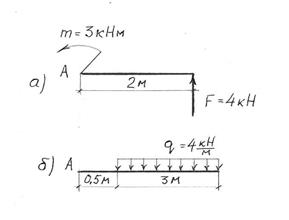Найти моменты сил относительно точки А (рис. 17).

Ответ: М_А= –11 кНм

Ответ: М_А= 24 кНм

рис.17

Условия равновесия произвольной плоской системы сил

Для произвольной плоской системы сил имеем три уравнения равновесия.

I вид

SF_x = 0

SF_y = 0 где А – любая точка на плоскости

SМ_А = 0

Для равновесия произвольной плоской системы сил необходимо, чтобы алгебраическая сумма проекций всех сил системы на каждую из двух координатных осей равнялась нулю и сумма моментов всех сил системы относительно любой точки равнялась нулю.

При решении некоторых задач одно или оба уравнения проекции целесообразно заменить уравнениями моментов относительно каких-либо точек.

II вид SFx = 0 SМА = 0 или SМВ = 0

III вид   SМА = 0 SМВ = 0 точки А, В и С не лежат на одной прямой SМС = 0