IV группа аксиом состоит из одной аксиомы - аксиомы непрерывности. Для любых непустых множеств X и Y из R таких, что для каждой пары элементов x  X и y
X и y  Y выполняется неравенство x < y, существует элемент a
Y выполняется неравенство x < y, существует элемент a 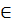 R, удовлетворяющий условию
R, удовлетворяющий условию
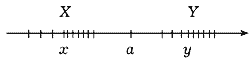 Рис. 2 Рис. 2 |
x < a < y, x  X, y
X, y  Y (рис.2). Перечисленные свойства полностью определяют множество действительных чисел в том смысле, что из этих свойств следуют и все остальные его свойства. Данное определение однозначно задает множество действительных чисел с точностью до конкретной природы его элементов. Оговорка о том, что в множестве содержится более одного элемента, необходима потому, что множество, состоящее из одного только нуля, очевидным образом удовлетворяет всем аксиомам. В дальнейшем элементы множества R будем называть числами.
Y (рис.2). Перечисленные свойства полностью определяют множество действительных чисел в том смысле, что из этих свойств следуют и все остальные его свойства. Данное определение однозначно задает множество действительных чисел с точностью до конкретной природы его элементов. Оговорка о том, что в множестве содержится более одного элемента, необходима потому, что множество, состоящее из одного только нуля, очевидным образом удовлетворяет всем аксиомам. В дальнейшем элементы множества R будем называть числами.
Свойство непрерывности вещественных чисел означает, что на вещественной прямой нет «пустот», то есть точки, изображающие числа заполняют всю вещественную ось.
Дадим другую формулировку аксиоме непрерывности (Юлиус Вильгельм Рихард Дедекинд (6 октября 1831 — 12 февраля 1916) — немецкий математик). Для этого введем определение
Два множества A и B будем называть сечением множества вещественных чисел, если
1) множества A и B не пусты;
2) объединение множеств A и B составляет множество всех вещественных чисел;
3) каждое число множества A меньше числа множества B.
То есть каждое множество, образующее сечение, содержит хотя бы один элемент, эти множества не содержат общих элементов и, если a ∈ A и b ∈ B, то a < b.
Множество A будем называть нижним классом, а множество B – верхним классом сечения. Обозначать сечение будем через 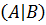 . Самыми простыми примерами сечений являются сечения полученные следующим образом. Возьмем какое - либо число α и положим A={x: x < α}, B={x: x ≥ α}. Легко видеть, что эти множества не пусты, не пересекаются и если a∈A и b∈B, то a < b, поэтому множества A и B образуют сечение. Аналогично можно образовать сечение множествами A ={x: x ≤ α}, B ={x: x > α}. Такие сечения будем называть сечениями, порожденными числом α или будем говорить, что число α производит это сечение. Это можно записать как α =
. Самыми простыми примерами сечений являются сечения полученные следующим образом. Возьмем какое - либо число α и положим A={x: x < α}, B={x: x ≥ α}. Легко видеть, что эти множества не пусты, не пересекаются и если a∈A и b∈B, то a < b, поэтому множества A и B образуют сечение. Аналогично можно образовать сечение множествами A ={x: x ≤ α}, B ={x: x > α}. Такие сечения будем называть сечениями, порожденными числом α или будем говорить, что число α производит это сечение. Это можно записать как α = 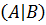 .
.
Сечения, порожденные каким-либо числом, обладают двумя интересными свойствами:
Свойство 1. Либо верхний класс содержит наименьше число, и в нижнем классе нет наибольшего числа, либо нижний класс содержит наибольшее число, и верхнем классе нет наименьшего.
Свойство 2. Число, производящее данное сечение, единственно.
Оказывается, что аксиома непрерывности, сформулированная выше, эквивалентна утверждению, которое называют принципом Дедекинда:
Принцип Дедекинда. Для каждого сечения существует число, порождающее это сечение.
Докажем эквивалентность этих утверждений.
► Пусть аксиома непрерывности справедлива и 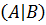 – какое либо заданное сечение. Принимая во внимание тот факт, что классы A и B удовлетворяют условиям аксиомы, можно утверждать существование числа λ, удовлетворяющего неравенству a ≤ λ ≤ b для любых чисел a ∈ A и b ∈ B. Однако, число λ должно принадлежать одному и только одному из классов A или B, поэтому будет выполнено одно из неравенств a ≤ λ < b или a < λ ≤ b. Следовательно число λ либо является наибольшим в нижнем классе, либо - наименьшим в верхнем классе и порождает данное сечение.
– какое либо заданное сечение. Принимая во внимание тот факт, что классы A и B удовлетворяют условиям аксиомы, можно утверждать существование числа λ, удовлетворяющего неравенству a ≤ λ ≤ b для любых чисел a ∈ A и b ∈ B. Однако, число λ должно принадлежать одному и только одному из классов A или B, поэтому будет выполнено одно из неравенств a ≤ λ < b или a < λ ≤ b. Следовательно число λ либо является наибольшим в нижнем классе, либо - наименьшим в верхнем классе и порождает данное сечение.
Обратно, пусть выполнен принцип Дедекинда и заданы два непустых множества A и B таких, что для всех a ∈ A и b ∈ B выполняется неравенство a≤ b. Обозначим через 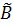 множество чисел
множество чисел 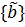 таких, что a ≤
таких, что a ≤ 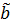 для любого
для любого 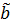 ∈
∈ 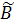 и всех a ∈ A. Тогда B ⊂
и всех a ∈ A. Тогда B ⊂ 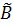 . За множество
. За множество 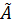 примем множество всех чисел, не входящих в
примем множество всех чисел, не входящих в 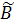 . Докажем, что множества
. Докажем, что множества 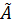 и
и 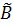 образуют сечение. Действительно, очевидно, что множество
образуют сечение. Действительно, очевидно, что множество 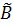 не пусто, так как содержит непустое множество B. Множество
не пусто, так как содержит непустое множество B. Множество 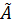 тоже не пусто, так как если число a ∈ A, то число a−1∉
тоже не пусто, так как если число a ∈ A, то число a−1∉ 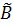 , так как любое число, входящее в
, так как любое число, входящее в 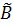 должно быть не меньше числа a, следовательно, a−1∈
должно быть не меньше числа a, следовательно, a−1∈ 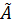 .
.
Далее, множества 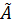 и
и 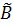 не пересекаются, и их объединение составляет множество всех вещественных чисел, в силу выбора множеств.
не пересекаются, и их объединение составляет множество всех вещественных чисел, в силу выбора множеств.
И, наконец, если 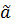 ∈
∈ 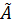 и
и 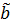 ∈
∈ 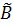 , то
, то 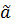 ≤
≤ 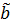 . Действительно, если какое- либо число c будет удовлетворять неравенству c >
. Действительно, если какое- либо число c будет удовлетворять неравенству c > 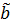 , где
, где 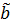 ∈
∈ 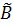 , то будет верным неравенство c > a (a - произвольный элемент множества A) и c ∈
, то будет верным неравенство c > a (a - произвольный элемент множества A) и c ∈ 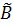 .
.
Итак, 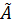 и
и 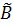 образуют сечение, и в силу принципа Дедекинда, существует число λ, порождающее это сечение, то есть являющееся либо наибольшим в классе
образуют сечение, и в силу принципа Дедекинда, существует число λ, порождающее это сечение, то есть являющееся либо наибольшим в классе 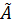 , либо наименьшим в классе
, либо наименьшим в классе 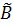 .
.
Докажем, что это число не может принадлежать классу 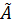 . Действительно, если λ ∈
. Действительно, если λ ∈ 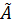 , то существует число a* ∈ A такое, что λ < a*. Тогда существует число a′, лежащее между числами λ и a*. Из неравенства a′ < a* следует, что a′ ∈
, то существует число a* ∈ A такое, что λ < a*. Тогда существует число a′, лежащее между числами λ и a*. Из неравенства a′ < a* следует, что a′ ∈ 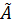 , тогда из неравенства λ < a′ следует, что λ не является наибольшим в классе
, тогда из неравенства λ < a′ следует, что λ не является наибольшим в классе 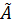 , что противоречит принципу Дедекинда. Следовательно, число λ будет наименьшим в классе
, что противоречит принципу Дедекинда. Следовательно, число λ будет наименьшим в классе 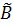 и для всех a ∈ A и будет выполняться неравенство a ≤ λ ≤ b, что и требовалось доказать.◄
и для всех a ∈ A и будет выполняться неравенство a ≤ λ ≤ b, что и требовалось доказать.◄
Таким образом, аксиома непрерывности и принцип Дедекинда эквивалентны. В дальнейшем аксиому непрерывности множества вещественных чисел мы будем называть непрерывностью по Дедекинду.
 2015-10-16
2015-10-16 957
957