Натуральные, целые и иррациональные числа

Определим теперь знакомые нам понятия натуральных, рациональных и иррациональных чисел. Числа 1, 2 1+1, 3 2+1,...называются натуральными числами, и их множество обозначается N. Из определения множества натуральных чисел вытекает, что оно обладает следующим характеристическим свойством: если

1) A 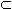N,

2) 1 A,

3) для каждого элемента x A имеет место включение x+ 1 A, то A = N.

Действительно, согласно условию 2) имеем 1 A, поэтому по свойству 3) и 2 A, а тогда согласно тому же свойству получим 3 A. Поскольку любое натуральное число n получается из 1 последовательным прибавлением к ней той же 1, то n A, т.е. N 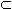A, а так как по условию 1 выполняется включение A 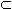N, то A = N.

На этом свойстве натуральных чисел основан принцип доказательства методом математической индукции. Если имеется множество утверждений, каждому из которых приписано натуральное число (его номер) n =1, 2,..., и если доказано, что:

1) справедливо утверждение с номером 1;

2) из справедливости утверждения с любым номером n N следует справедливость утверждения с номером n +1;

то тем самым доказана справедливость всех утверждений, т.е. любого утверждения с произвольным номером n N.

Числа 0, + 1, + 2,... называют целыми числами, их множество обозначают Z.

Числа вида m/n, где m и n целые, а n 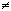0, называются рациональными числами. Множество всех рациональных чисел обозначают Q.

Действительные числа, не являющиеся рациональными, называются иррациональными, их множество обозначается I.