2015-10-16
6045
Из непрерывности множества вещественных чисел по Дедекинду следует важная теорема:
Теорема 4.2.1 (Принцип Архимеда). Каково бы ни было вещественное число a, существует натуральное число n такое, что a < n.
Доказательство.► Допустим, что утверждение теоремы неверно, то есть существует такое число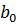 
, что выполняется неравенство n ≤ 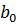для всех натуральных чисел n. Разобьем множество вещественных чисел на два класса: в класс B отнесем все числа b, удовлетворяющие неравенству n ≤ b для любых натуральных n. Этот класс не пуст, так как ему принадлежит число 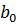. В класс A отнесем все оставшиеся числа. Этот класс тоже не пуст, так как любое натуральное число входит в A. Классы A и B не пересекаются и их объединение составляет множество всех вещественных чисел.
Если взять произвольные числа a ∈ A и b ∈ B, то найдется натуральное число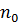 
такое, что a < 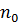≤ b, откуда следует, что a < b. Следовательно, классы A и B удовлетворяют принципу Дедекинда и существует число α, которое порождает сечение 
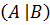, то есть α является либо наибольшим в классе A, либо наименьшим в классе B. Если предположить, что α входит в класс A, то можно найти натуральное 
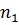, для которого выполняется неравенство α < 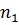. Так как 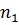тоже входит в A, то число α не будет наибольшим в этом классе, следовательно, наше предположение неверно и α является наименьшим в классе B.
|
|
|
С другой стороны, возьмем число α−1, которое входит в класс A. Следовательно, найдется натуральное число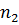 
такое, что α − 1 < 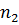, откуда получим α < 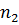+ 1. Так как 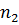+ 1 - натуральное число, то из последнего неравенства следует, что α ∈ A. Полученное противоречие доказывает теорему.◄
Следствие. Каковы бы ни были числа a и b такие, что 0 < a < b, существует натуральное число n, для которого выполняется неравенство na > b. ►Для доказательства достаточно применить принцип Архимеда к числу b/a и воспользоваться свойством неравенств.◄
Это следствие имеет простой геометрический смысл - каковы бы ни были два отрезка, если на большем из них, от одного из его концов последовательно откладывать меньший, то за конечное число шагов можно выйти за пределы большего отрезка.
