В школьном курсе математики действительные числа определялись конструктивным путем, основываясь на потребности проводить измерения. Такое определение являлось нестрогим и часто заводило исследователей в тупик. Например, вопрос о непрерывности действительных чисел, то есть имеются ли пустоты в этом множестве. Поэтому при проведении математических исследований необходимо иметь строгое определение исследуемых понятий, хотя бы в рамках некоторых интуитивных предположений (аксиом), которые согласуются с практикой.
О п р е д е л е н и е. Совокупность элементов x, y, z, …, состоящая более чем из одного элемента, называется множеством R действительных чисел, если для этих объектов установлены следующие операции и отношения:
I группа аксиом – аксиомы операции сложения.
В множестве R введена операция сложения, то есть для любой пары элементов a и b определен единственный элемент, называемый их суммой и обозначаемый a + b, так, что при этом выполняются следующие условия:
I1. a + b = b + a, a, b  R.
R.
I2. a +(b+c)=(a+b)+ c, a, b, c  R.
R.
I3. Существует такое элемент, называемый нулем и обозначаемый 0, что для любого a  R выполняется условие a +0= a.
R выполняется условие a +0= a.
I4. Для любого элемента a  R существует элемент, называемый ему противоположным и обозначаемый - a, для которого a +(- a)=0. Элемент a +(- b), a, b
R существует элемент, называемый ему противоположным и обозначаемый - a, для которого a +(- a)=0. Элемент a +(- b), a, b  R, называется разностью элементов a и b и обозначается a - b.
R, называется разностью элементов a и b и обозначается a - b.
II –группа аксиом - аксиомы операции умножения. В множестве R введена операция умножения, то есть для любой пары элементов a и b определен единственный элемент, называемый их произведением и обозначаемый a b, так, что при этом выполняются следующие условия:
II1. ab = ba, a, b  R.
R.
II2 a (bc)=(ab) c, a, b, c  R.
R.
II3. Существует такое элемент, называемое единицей и обозначаемое 1, что для любого a  R выполняется условие a
R выполняется условие a  1= a.
1= a.
II4. Для любого a 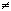 0 существует элемент, называемый ему обратным и обозначаемый
0 существует элемент, называемый ему обратным и обозначаемый 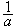 или 1/ a, для которого a
или 1/ a, для которого a 
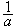 =1. Элемент a
=1. Элемент a 
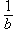 , b
, b 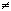 0, называется частным от деления a на b и обозначается a: b или
0, называется частным от деления a на b и обозначается a: b или 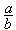 или a / b.
или a / b.
II5. Связь операций сложения и умножения: для любых a, b, c  R выполняется условие (ac + b)c = ac+bc.
R выполняется условие (ac + b)c = ac+bc.
Совокупность объектов, удовлетворяющая аксиомам I и II групп, называются числовым полем или просто полем. А соответствующие аксиомы называются аксиомами поля.
III – третья группа аксиом - аксиомы порядка. Для элементов R определено отношение порядка. Оно состоит в следующем. Для любых двух различных элементов a и b имеет место одно из двух соотношений: либо a 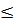 b (читается " a меньше или равно b "), либо a
b (читается " a меньше или равно b "), либо a 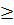 b (читается " a больше или равно b "). При этом предполагается, что выполняются следующие условия:
b (читается " a больше или равно b "). При этом предполагается, что выполняются следующие условия:
III1. a 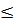 a для каждого a. Из a
a для каждого a. Из a 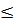 b, b
b, b 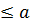 следует a=b.
следует a=b.
III2. Транзитивность. Если a 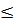 b и b
b и b 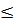 c, то a
c, то a 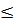 c.
c.
III3. Если a 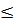 b, то для любого элемента c имеет место a + c
b, то для любого элемента c имеет место a + c 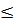 b + c.
b + c.
III4. Если a 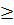 0, b
0, b 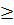 0, то ab
0, то ab 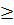 0.
0.
IV группа аксиом состоит из одной аксиомы - аксиомы непрерывности. Для любых непустых множеств X и Y из R таких, что для каждой пары элементов x  X и y
X и y  Y выполняется неравенство x < y, существует элемент a
Y выполняется неравенство x < y, существует элемент a 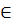 R, удовлетворяющий условию
R, удовлетворяющий условию
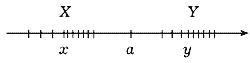 Рис. 2 Рис. 2 |
x < a < y, x  X, y
X, y  Y (рис.2). Перечисленные свойства полностью определяют множество действительных чисел в том смысле, что из этих свойств следуют и все остальные его свойства. Данное определение однозначно задает множество действительных чисел с точностью до конкретной природы его элементов. Оговорка о том, что в множестве содержится более одного элемента, необходима потому, что множество, состоящее из одного только нуля, очевидным образом удовлетворяет всем аксиомам. В дальнейшем элементы множества R будем называть числами.
Y (рис.2). Перечисленные свойства полностью определяют множество действительных чисел в том смысле, что из этих свойств следуют и все остальные его свойства. Данное определение однозначно задает множество действительных чисел с точностью до конкретной природы его элементов. Оговорка о том, что в множестве содержится более одного элемента, необходима потому, что множество, состоящее из одного только нуля, очевидным образом удовлетворяет всем аксиомам. В дальнейшем элементы множества R будем называть числами.
Определим теперь знакомые нам понятия натуральных, рациональных и иррациональных чисел. Числа 1, 2  1+1, 3
1+1, 3  2+1,...называются натуральными числами, и их множество обозначается N. Из определения множества натуральных чисел вытекает, что оно обладает следующим характеристическим свойством: если
2+1,...называются натуральными числами, и их множество обозначается N. Из определения множества натуральных чисел вытекает, что оно обладает следующим характеристическим свойством: если
1) A  N,
N,
2) 1  A,
A,
3) для каждого элемента x  A имеет место включение x+ 1
A имеет место включение x+ 1  A, то A = N.
A, то A = N.
Действительно, согласно условию 2) имеем 1  A, поэтому по свойству 3) и 2
A, поэтому по свойству 3) и 2  A, а тогда согласно тому же свойству получим 3
A, а тогда согласно тому же свойству получим 3  A. Поскольку любое натуральное число n получается из 1 последовательным прибавлением к ней той же 1, то n
A. Поскольку любое натуральное число n получается из 1 последовательным прибавлением к ней той же 1, то n  A, т.е. N
A, т.е. N  A, а так как по условию 1 выполняется включение A
A, а так как по условию 1 выполняется включение A  N, то A = N.
N, то A = N.
На этом свойстве натуральных чисел основан принцип доказательства методом математической индукции. Если имеется множество утверждений, каждому из которых приписано натуральное число (его номер) n =1, 2,..., и если доказано, что:
1) справедливо утверждение с номером 1;
2) из справедливости утверждения с любым номером n  N следует справедливость утверждения с номером n +1;
N следует справедливость утверждения с номером n +1;
то тем самым доказана справедливость всех утверждений, т.е. любого утверждения с произвольным номером n  N.
N.
Числа 0, + 1, + 2,... называют целыми числами, их множество обозначают Z.
Числа вида m/n, где m и n целые, а n 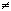 0, называются рациональными числами. Множество всех рациональных чисел обозначают Q.
0, называются рациональными числами. Множество всех рациональных чисел обозначают Q.
Действительные числа, не являющиеся рациональными, называются иррациональными, их множество обозначается I.
Возникает вопрос, что, может быть, рациональные числа исчерпывают все элементы множества R? Ответ на этот вопрос дает аксиома непрерывности. Действительно, для рациональных чисел эта аксиома не выполняется. Для примера, рассмотрим два множества:
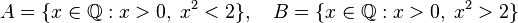
Легко видеть, что для любых элементов 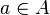 и
и 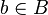 выполняется неравенство
выполняется неравенство 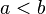 . Однако рационального числа
. Однако рационального числа 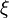 , разделяющего эти два множества, не существует. В самом деле, этим числом может быть только
, разделяющего эти два множества, не существует. В самом деле, этим числом может быть только 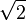 , но оно не является рациональным. Этот факт и указывает на то, что существуют иррациональные числа в множестве R.
, но оно не является рациональным. Этот факт и указывает на то, что существуют иррациональные числа в множестве R.
Кроме четырех арифметических действий над числами можно производить действия возведения в степень и извлечения корня. Для любого числа a  R и натурального n степень an определяется как произведение n сомножителей, равных a:
R и натурального n степень an определяется как произведение n сомножителей, равных a: 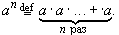
По определению a 0  1, a >0, a -n
1, a >0, a -n  1/ a n, a
1/ a n, a 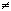 0, n - натуральное число.
0, n - натуральное число.
Пример. Неравенство Бернулли: (1+x)n > 1+nx Доказать методом индукции.
Пусть a >0, n - натуральное число. Число b называется корнем n -й степени из числа a, если bn=a. В этом случае пишется 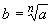 . Существование и единственность положительного корня любой степени n из любого положительного числа будет доказано ниже в п. 7.3.
. Существование и единственность положительного корня любой степени n из любого положительного числа будет доказано ниже в п. 7.3.
Корень четной степени 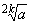 , a
, a 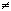 0, имеет два значения: если b =
0, имеет два значения: если b = 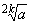 , k
, k  N, то и -b =
N, то и -b = 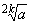 . Действительно, из b2k = a следует, что
. Действительно, из b2k = a следует, что
(-b) 2k = ((-b) 2) k = (b2) k = b2k
Неотрицательное значение 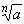 называется его арифметическим значением.
называется его арифметическим значением.
Если r = p/q, где p и q целые, q 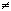 0, т. е. r - рациональное число, то для a > 0
0, т. е. r - рациональное число, то для a > 0
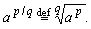 | (2.1) |
Таким образом, степень ar определена для любого рационального числа r. Из ее определения следует, что для любого рационального r имеет место равенство
a-r = 1/ ar.
Степень ax (число x называется показателем степени) для любого действительного числа x получается с помощью непрерывного распространения степени с рациональным показателем (см. об этом в п. 8.2). Для любого числа a  R неотрицательное число
R неотрицательное число
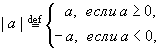
называется его абсолютной величиной или модулем. Для абсолютных величин чисел справедливы неравенства
| a + b | < | a | + | b |,
|| a - b || < | a - b |, a, b  R
R
Они доказываются с помощью свойств I-IV действительных чисел.
Роль аксиомы непрерывности в построении математического анализа[править | править вики-текст]
Значение аксиомы непрерывности таково, что без нее невозможно строгое построение математического анализа.[ источник не указан 1351 день ] Для иллюстрации приведем несколько фундаментальных утверждений анализа, доказательство которых опирается на непрерывность действительных чисел:
· (Теорема Вейерштрасса). Всякая ограниченная монотонно возрастающая последовательность сходится
· (Теорема Больцано — Коши). Непрерывная на отрезке функция, принимающая на его концах значения разного знака, обращается в нуль в некоторой внутренней точке отрезка
· (Существование степенной, показательной, логарифмической и всех тригонометрических функций на всей «естественной» области определения). Например, доказывается, что для всякого 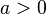 и целого
и целого 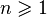 существует
существует 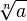 , то есть решение уравнения
, то есть решение уравнения 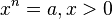 . Это позволяет определить значение выражения
. Это позволяет определить значение выражения 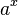 для всех рациональных
для всех рациональных 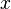 :
:
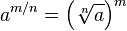
Наконец, снова благодаря непрерывности числовой прямой можно определить значение выражения 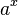 уже для произвольного
уже для произвольного 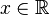 . Аналогично, используя свойство непрерывности, доказывается существование числа
. Аналогично, используя свойство непрерывности, доказывается существование числа 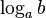 для любых
для любых 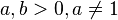 .
.
Длительный исторический промежуток времени математики доказывали теоремы из анализа, в «тонких местах» ссылаясь на геометрическое обоснование, а чаще — и вовсе их пропуская поскольку это было очевидно. Важнейшее понятие непрерывности использовалось без какого-либо четкого определения. Лишь в последней трети XIX века немецкий математик Карл Вейерштрасс произвел арифметизацию анализа, построив первую строгую теорию действительных чисел как бесконечных десятичных дробей. Он предложил классическое определение предела на языке 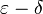 , доказал ряд утверждений, которые до него считались «очевидными», и тем самым завершил построение фундамента математического анализа.
, доказал ряд утверждений, которые до него считались «очевидными», и тем самым завершил построение фундамента математического анализа.
Позднее были предложены другие подходы к определению действительного числа. В аксиоматическом подходе непрерывность действительных чисел выделена явно в отдельную аксиому. В конструктивных подходах к теории действительного числа, например при построении действительных чисел с помощью дедекиндовых сечений, свойство непрерывности (в той или иной формулировке) доказывается в качестве теоремы.
Другие формулировки свойства непрерывности и эквивалентные предложения[править | править вики-текст]
Существует несколько различных утверждений, выражающих свойство непрерывности действительных чисел. Каждый из этих принципов можно положить в основу построения теории действительного числа в качестве аксиомы непрерывности, и из него вывести все остальные[4][5]. Подробнее этот вопрос обсуждается в следующем разделе.
Непрерывность по Дедекинду [править | править вики-текст]
Основная статья: Теория сечений в области рациональных чисел
Вопрос о непрерывности действительных чисел Дедекинд рассматривает в своей работе «Непрерывность и иррациональные числа» [6]. В ней он сравнивает рациональные числа с точками прямой линии. Как известно, между рациональными числами и точками прямой можно установитьсоответствие, когда на прямой выбирают начальную точку и единицу измерения отрезков. При помощи последней можно по каждому рациональному числу 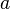 построить соответствующий отрезок, и отложив его вправо или влево, смотря по тому, есть ли
построить соответствующий отрезок, и отложив его вправо или влево, смотря по тому, есть ли 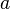 положительное или отрицательное число, получить точку
положительное или отрицательное число, получить точку 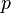 , соответствующую числу
, соответствующую числу 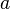 . Таким образом, каждому рациональному числу
. Таким образом, каждому рациональному числу 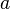 соответствует одна и только одна точка
соответствует одна и только одна точка 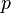 на прямой.
на прямой.
При этом оказывается, что на прямой имеется бесконечно много точек, которые не соответствуют никакому рациональному числу. Например, точка, полученная путем отложения длины диагонали квадрата построенного на единичном отрезке. Таким образом, область рациональных чисел не обладает той полнотой, или же непрерывностью, которая присуща прямой линии.
 | Предыдущее сравнение области рациональных чисел с прямой привело к открытию в первой изъянов (Lückenhaftigkeit), неполноты, или разрывности, между тем как прямой мы приписываем полноту, отсутствие пробелов, непрерывность. Р. Дедекинд, «Непрерывность и иррациональные числа» |  |
Чтобы выяснить в чем же состоит эта непрерывность, Дедекинд делает следующее замечание. Если 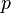 есть определенная точка прямой, то все точки прямой распадаются на два класса: точки расположенные левее
есть определенная точка прямой, то все точки прямой распадаются на два класса: точки расположенные левее 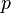 , и точки расположенные правее
, и точки расположенные правее 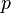 . Сама же точка
. Сама же точка 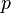 может быть произвольно отнесена либо к нижнему, либо к верхнему классу. Дедекинд усматривает сущность непрерывности в обратном принципе:
может быть произвольно отнесена либо к нижнему, либо к верхнему классу. Дедекинд усматривает сущность непрерывности в обратном принципе:
 | Если точки прямой распадаются на два класса такого рода, что каждая точка первого класса лежит влево от каждой точки второго класса, то существует одна и только одна точка, которая производит это разделение прямой на два класса, это рассечение прямой на два куска. Р. Дедекинд, «Непрерывность и иррациональные числа» |  |
Геометрически этот принцип представляется очевидным, однако доказать его мы не в состоянии. Дедекинд подчеркивает, что, по существу, этот принцип является постулатом, в котором выражена сущность того приписываемого прямой свойства, которое мы называем непрерывностью.
 | Принятие этого свойства прямой линии есть ни что иное, как аксиома, посредством которой мы только и признаем за прямой ее непрерывность, мысленно вкладываем непрерывность в прямую. Р. Дедекинд, «Непрерывность и иррациональные числа» |  |
Скачок
Пробел
Чтобы глубже понять сущность непрерывности числовой прямой в смысле Дедекинда, рассмотрим произвольноесечение множества действительных чисел, то есть разделение всех действительных чисел на два непустых класса, так что все числа одного класса лежат на числовой прямой левее всех чисел второго. Эти классы называются соответственно нижним и верхним классами сечения. Теоретически имеются 4 возможности:
1. В нижнем классе есть максимальный элемент, в верхнем классе нет минимального
2. В нижнем классе нет максимального элемента, а в верхнем классе есть минимальный
3. В нижнем классе есть максимальный, а в верхнем — минимальный элементы
4. В нижнем классе нет максимального, а в верхнем — минимального элементов
В первом и втором случаях максимальный элемент нижнего или минимальный элемент верхнего соответственно и производит данное сечение. В третьем случае мы имеем скачок, а в четвертом — пробел. Таким образом, непрерывность числовой прямой означает, что в множестве действительных чисел нет ни скачков, ни пробелов, то есть, образно говоря, нет пустот.
Если ввести понятие сечения множества действительных чисел, то принцип непрерывности Дедекинда можно сформулировать так.
Принцип непрерывности Дедекинда (полноты). Для каждого сечения множества действительных чисел существует число, производящее это сечение.
Замечание. Формулировка Аксиомы непрерывности о существовании точки, разделяющей два множества, весьма напоминает формулировку принципа непрерывности Дедекинда. В действительности, эти утверждения эквивалентны, и, по существу, являются разными формулировками одного и того же. Поэтому оба эти утверждения называют принципом непрерывности действительных чисел по Дедекинду.
Лемма о вложенных отрезках (принцип Коши — Кантора) [править | править вики-текст]
Основная статья: Лемма о вложенных отрезках
Лемма о вложенных отрезках (Коши — Кантор). Всякая система вложенных отрезков
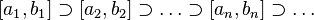
имеет непустое пересечение, то есть существует по крайней мере одно число, принадлежащее всем отрезкам данной системы.
Если, кроме того, длина отрезков данной системы стремится к нулю, то есть
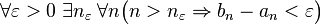
то пересечение отрезков данной системы состоит из одной точки.
Это свойство называют непрерывностью множества действительных чисел в смысле Кантора. Ниже будет показано, что для архимедовыхупорядоченных полей непрерывность по Кантору эквивалентна непрерывности по Дедекинду.
Принцип супремума [править | править вики-текст]
Принцип супремума. Всякое непустое ограниченное сверху множество действительных чисел имеет супремум.
В курсах математического анализа это предложение обычно является теоремой и его доказательство существенно использует непрерывность множества действительных чисел в той или иной форме. Вместе с тем можно наоборот, постулировать существование супремума у всякого непустого ограниченного сверху множества, и опираясь на это доказать, например, принцип непрерывности по Дедекинду. Таким образом, теорема о супремуме является одной из эквивалентных формулировок свойства непрерывности действительных чисел.
Замечание. Вместо супремума можно использовать двойственное понятие инфимума.
Принцип инфимума. Всякое непустое ограниченное снизу множество действительных чисел имеет инфимум.
Это предложение также эквивалентно принципу непрерывности Дедекинда. Более того можно показать, что из утверждения теоремы о супремуме непосредственно вытекает утверждение теоремы об инфимуме, и наоборот (см. ниже).
Лемма о конечном покрытии (принцип Гейне — Бореля) [править | править вики-текст]
Основная статья: Лемма Гейне — Бореля
Лемма о конечном покрытии (Гейне — Борель). В любой системе интервалов, покрывающей отрезок, существует конечная подсистема, покрывающая этот отрезок.
Лемма о предельной точке (принцип Больцано — Вейерштрасса) [править | править вики-текст]
Основная статья: Теорема Больцано — Вейерштрасса
Лемма о предельной точке (Больцано — Вейерштрасс). Всякое бесконечное ограниченное числовое множество имеет по крайней мере одну предельную точку.
Эквивалентность предложений, выражающих непрерывность множества действительных чисел[править | править вики-текст]
Сделаем некоторые предварительные замечания. В соответствии с аксиоматическим определением действительного числа, совокупность действительных чисел удовлетворяет трем группам аксиом. Первая группа — аксиомы поля. Вторая группа выражает тот факт, что совокупность действительных чисел есть линейно упорядоченное множество, причем отношение порядка согласовано с основными операциями поля. Таким образом, первая и вторая группы аксиом означают, что совокупность действительных чисел представляет собой упорядоченное поле. Третья группа аксиом состоит из одной аксиомы — аксиомы непрерывности (или, полноты).
Чтобы показать эквивалентность различных формулировок непрерывности действительных чисел, следует доказать, что если для упорядоченого поля выполнено одно из этих предложений, то из этого вытекает справедливость всех остальных.
Теорема. Пусть  — произвольное линейно упорядоченное множество. Следующие утверждения эквивалентны:
— произвольное линейно упорядоченное множество. Следующие утверждения эквивалентны:
1. Каковы бы ни были непустые множества  и
и 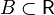 , такие что для любых двух элементов
, такие что для любых двух элементов 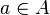 и
и 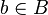 выполняется неравенство
выполняется неравенство 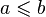 , существует такой элемент
, существует такой элемент 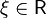 , что для всех
, что для всех 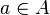 и
и 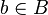 имеет место соотношение
имеет место соотношение
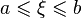
2. Для всякого сечения в 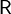 существует элемент, производящий это сечение
существует элемент, производящий это сечение
3. Всякое непустое ограниченное сверху множество 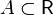 имеет супремум
имеет супремум
4. Всякое непустое ограниченное снизу множество 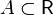 имеет инфимум
имеет инфимум
Как видно из этой теоремы, эти четыре предложения используют лишь то, что на 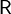 введено отношение линейного порядка, и не используют структуру поля. Таким образом, каждое из них выражает свойство
введено отношение линейного порядка, и не используют структуру поля. Таким образом, каждое из них выражает свойство 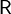 как линейно упорядоченного множества. Это свойство (произвольного линейно упорядоченного множества, не обязательно множества действительных чисел) называется непрерывностью, или полнотой, по Дедекинду.
как линейно упорядоченного множества. Это свойство (произвольного линейно упорядоченного множества, не обязательно множества действительных чисел) называется непрерывностью, или полнотой, по Дедекинду.
Доказательство эквивалентности других предложений уже требует наличия структуры поля.
Теорема. Пусть 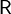 — произвольное упорядоченное поле. Следующие предложения равносильны:
— произвольное упорядоченное поле. Следующие предложения равносильны:
1. 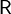 (как линейно упорядоченное множество) является полным по Дедекинду
(как линейно упорядоченное множество) является полным по Дедекинду
2. Для 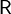 выполнены принцип Архимеда и принцип вложенных отрезков
выполнены принцип Архимеда и принцип вложенных отрезков
3. Для 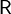 выполнен принцип Гейне — Бореля
выполнен принцип Гейне — Бореля
4. Для 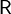 выполнен принцип Больцано — Вейерштрасса
выполнен принцип Больцано — Вейерштрасса
Замечание. Как видно из теоремы, принцип вложенных отрезков сам по себе не равносилен принципу непрерывности Дедекинда. Из принципа непрерывности Дедекинда следует принцип вложенных отрезков, однако для обратного требуется дополнительно потребовать, чтобы упорядоченное поле 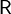 удовлетворяло аксиоме Архимеда
удовлетворяло аксиоме Архимеда
Доказательство приведенных теорем можно найти в книгах из списка литературы, приведенного ниже.
· Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — 704 с. — ISBN 5-7107-4119-1.
· Фихтенгольц, Г. М. Основы математического анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2002. — Т. 1. — 416 с. — ISBN 5-9221-0196-X.
· Дедекинд, Р. Непрерывность и иррациональные числа = Stetigkeit und irrationale Zahlen. — 4-е исправленное издание. — Одесса: Mathesis, 1923. — 44 с.
· Зорич, В. А. Математический анализ. Часть I. — Изд. 4-е, испр.. — М.: «МЦНМО», 2002. — 657 с. — ISBN 5-94057-056-9.
· Непрерывность функций и числовых областей: Б. Больцано, Л. О. Коши, Р. Дедекинд, Г. Кантор. — 3-е изд. — Новосибирск: АНТ, 2005. — 64 с.
4.5. Аксиома непрерывности
Каковы бы ни были два непустых множества вещественных чисел A и
B, у которых для любых элементов a ∈ A и b ∈ B выполняется неравенство
a ≤ b, существует такое число λ, что для всех a ∈ A, b ∈ B имеет место не-
равенство a ≤ λ ≤ b.
Свойство непрерывности вещественных чисел означает, что на вещест-
венной прямой нет «пустот», то есть точки, изображающие числа заполняют
всю вещественную ось.
Дадим другую формулировку аксиоме непрерывности. Для этого введем
Определение 1.4.5. Два множества A и B будем называть сечением
множества вещественных чисел, если
1) множества A и B не пусты;
2) объединение множеств A и B составляет множество всех веществен-
ных чисел;
3) каждое число множества A меньше числа множества B.
То есть каждое множество, образующее сечение, содержит хотя бы один
элемент, эти множества не содержат общих элементов и, если a ∈ A и b ∈ B, то
a < b.
Множество A будем называть нижним классом, а множество B - верхним
классом сечения. Обозначать сечение будем через A B.
Самыми простыми примерами сечений являются сечения полученные сле-
дующим образом. Возьмем какое- либо число α и положим
A = { x x < α }, B = { x x ≥ α }. Легко видеть, что эти множества не пусты, не пере-
секаются и если a ∈ A и b ∈ B, то a < b, поэтому множества A и B образуют
сечение. Аналогично, можно образовать сечение, множествами
A ={x x ≤ α }, B ={x x > α }.
Такие сечения будем называть сечениями, порожденными числом α или
будем говорить, что число α производит это сечение. Это можно записать как
α = A B.
Сечения, порожденные каким-либо числом, обладают двумя интересными
свойствами:
Свойство 1. Либо верхний класс содержит наименьше число, и в нижнем
классе нет наибольшего числа, либо нижний класс содержит наибольшее чис-
ло, и верхнем классе нет наименьшего.
Свойство 2. Число, производящее данное сечение, единственно.
Оказывается, что аксиома непрерывности, сформулированная выше, эквива-
лентна утверждению, которое называют принципом Дедекинда:
Принцип Дедекинда. Для каждого сечения существует число, порождающее
это сечение.
Докажем эквивалентность этих утверждений.
► Пусть справедлива аксиома непрерывности, и задано какое-нибудь се-
чение A B. Тогда, так как классы A и B удовлетворяют условиям, сформули-
рованным в аксиоме, существует число λ такое, что a ≤ λ ≤ b для любых чисел
a ∈ A и b ∈ B. Но число λ должно принадлежать одному и только одному из
классов A или B, поэтому будет выполнено одно из неравенств a ≤ λ < b или
a < λ ≤ b. Таким образом, число λ либо является наибольшим в нижнем классе,
либо наименьшим в верхнем классе и порождает данное сечение.
Обратно, пусть выполнен принцип Дедекинда и заданы два непустых
множества A и B таких, что для всех a ∈ A и b ∈ B выполняется неравенство
{}
a ≤ b. Обозначим через B множество чисел b таких, что a ≤ b для любого
b ∈ B и всех a ∈ A. Тогда B ⊂ B. За множество A примем множество всех чи-
сел, не входящих в B.
Докажем, что множества A и B образуют сечение.
Действительно, очевидно, что множество B не пусто, так как содержит
непустое множество B. Множество A тоже не пусто, так как если число a ∈ A,
то число a − 1∉ B, так как любое число, входящее в B должно быть не меньше
числа a, следовательно, a − 1∈ A.
Далее, множества A и B не пересекаются, и их объединение составляет
множество всех вещественных чисел, в силу выбора множеств.
И, наконец, если a ∈ A и b ∈ B, то a ≤ b. Действительно, если какое- либо
число c будет удовлетворять неравенству c > b, где b ∈ B, то будет верным не-
равенство c > a (a - произвольный элемент множества A) и c ∈ B.
Итак, A и B образуют сечение, и в силу принципа Дедекинда, существует чис-
ло λ, порождающее это сечение, то есть являющееся либо наибольшим в клас-
се A, либо наименьшим в классе B.
Докажем, что это число не может принадлежать классу A. Действитель-
но, если λ ∈ A, то существует число a* ∈ A такое, что λ < a*. Тогда существует
число a′, лежащее между числами λ и a*. Из неравенства a′ < a* следует, что
a′ ∈ A, тогда из неравенства λ < a′ следует, что λ не является наибольшим в
классе A, что противоречит принципу Дедекинда. Следовательно, число λ бу-
дет наименьшим в классе B и для всех a ∈ A и будет выполняться неравенство
a ≤ λ ≤ b, что и требовалось доказать.◄
Таким образом, свойство, сформулированное в аксиоме и свойство,
сформулированное в принципе Дедекинда эквивалентны. В дальнейшем эти
свойства множества вещественных чисел мы будем называть непрерывностью
по Дедекинду.
Из непрерывности множества вещественных чисел по Дедекинду следуют
две важные теоремы.
Теорема 1.4.3. (Принцип Архимеда) Каково бы ни было вещественное число
a, существует натуральное число n такое, что a < n.
► Допустим, что утверждение теоремы неверно, то есть существует та-
кое число b0, что выполняется неравенство n ≤ b0 для всех натуральных чисел
n. Разобьем множество вещественных чисел на два класса: в класс B отнесем
все числа b, удовлетворяющие неравенству n ≤ b для любых натуральных n.
Этот класс не пуст, так как ему принадлежит число b0. В класс A отнесем все
оставшиеся числа. Этот класс тоже не пуст, так как любое натуральное число
входит в A. Классы A и B не пересекаются и их объединение составляет
множество всех вещественных чисел.
Если взять произвольные числа a ∈ A и b ∈ B, то найдется натуральное
число n0 такое, что a < n0 ≤ b, откуда следует, что a < b. Следовательно, классы
A и B удовлетворяют принципу Дедекинда и существует число α, которое
порождает сечение A B, то есть α является либо наибольшим в классе A, ли-
бо наименьшим в классе B. Если предположить, что α входит в класс A, то
можно найти натуральное n1, для которого выполняется неравенство α < n1.
Так как n1 тоже входит в A, то число α не будет наибольшим в этом классе,
следовательно, наше предположение неверно и α является наименьшим в
классе B.
С другой стороны, возьмем число α − 1, которое входит в класс A. Следова-
тельно, найдется натуральное число n2 такое, что α − 1 < n2, откуда получим
α < n2 + 1. Так как n2 + 1 - натуральное число, то из последнего неравенства
следует, что α ∈ A. Полученное противоречие доказывает теорему.◄
Следствие. Каковы бы ни были числа a и b такие, что 0 < a < b, существует
натуральное число n, для которого выполняется неравенство na > b.
►Для доказательства достаточно применить принцип Архимеда к числу
b
и воспользоваться свойством неравенств.◄
a
Следствие имеет простой геометрический смысл: Каковы бы ни были два
отрезка, если на большем из них, от одного из его концов последовательно от-
кладывать меньший, то за конечное число шагов можно выйти за пределы
большего отрезка.
Пример 1. Доказать, что для всякого неотрицательного числа a существует
единственное неотрицательное вещественное число t такое, что
t n = a, n ∈, n ≥ 2.
Эта теорема о существовании арифметического корня n-ой степени
из неотрицательного числа в школьном курсе алгебры принимается без дока-
зательства.
☺Если a = 0, то x = 0, поэтому доказательство существования арифмети-
ческого корня из числа a требуется только для a > 0.
Предположим, что a > 0 и разобьем множество всех вещественных чисел
на два класса. В класс B отнесем все положительные числа x, которые удовле-
творяют неравенству x n > a, в класс A, все остальные.
По аксиоме Архимеда существуют натуральные числа k и m такие, что
1 1 1
< a < k. Тогда k 2 ≥ k > a и 2 ≤ < a, т.е. оба класса непусты, причем класс
m m m
A содержит положительные числа.
Очевидно, что A ∪ B = и если x1 ∈ A и x2 ∈ B, то x1 < x2.
Таким образом, классы A и B образуют сечение. Число, образующее это
сечение, обозначим через t. Тогда t либо является наибольшим числом в клас-
се A, либо наименьшим в классе B.
Допустим, что t ∈ A и t n < a. Возьмем число h, удовлетворяющее нера-
венству 0 < h < 1. Тогда
(t + h)n = t n + Cnt n−1h + Cn t n−2h2 +... + Cnn hn < t n + Cnt n−1h + Cn t n−2h +... + Cn h =
1 2 1 2 n
= t n + h (Cnt n−1 + Cn t n−2 +... + Cn + Cn t n) − hCn t n = t n + h (t + 1) − ht n =
1 2 n 0 0 n
(
= t n + h (t + 1) − t n
n
)
a − tn
, то получим (t + h) < a. Это означает,
n
Отсюда, если взять h <
(t + 1)
−t
n n
что t + h ∈ A, что противоречит тому, что t наибольший элемент в классе A.
Аналогично, если предположить, что t - наименьший элемент класса B,
tn − a
то, взяв число h, удовлетворяющее неравенствам 0 < h < 1 и h <,
(t + 1) − t n
n
получим (t − h) = t n − Cnt n−1h + Cn t n−2 h 2 −... + (−1) Cn h n >
n 1 2 n n
() ()
> t n − Cnt n−1h + Cn t n−2h +... + Cn h = t n − h (t + 1) − t n > a.
1 2 n n
Это означает, что t − h ∈ B и t не может быть наименьшим элементом
класса B. Следовательно, t n = a.
Единственность следует из того что, если t1 < t2, то t1n < t2.☻ n
Пример 2. Доказать, что, если a < b, то всегда найдется рациональное число r
такое, что a < r < b.
a+b
☺Если числа a и b - рациональные, то число рационально и удов-
летворяет требуемым условиям. Допустим, что хотя бы одно из чисел a или b
иррационально, например, допустим, что иррационально число b. Предполо-
жим также, что a ≥ 0, тогда b > 0. Запишем представления чисел a и b в виде
десятичных дробей: a = α 0,α1α 2α 3.... и b = β 0, β1β 2 β3..., где вторая дробь беско-
нечная и непериодическая. Что касается представления числа a, то будем счи-
тать, что, если число a - рационально, то его запись либо конечна, либо это пе-
риодическая дробь, период которой не равен 9.
Так как b > a, то β 0 ≥ α 0; если β 0 = α 0, то β1 ≥ α1; если β1 = α1, то β 2 ≥ α 2
и т. д., причем найдется такое значение i, при котором в первый раз будет вы-
полняться строгое неравенство βi > α i. Тогда число β 0, β1β 2...βi будет рацио-
нальным и будет лежать между числами a и b.
Если a < 0, то приведенное рассуждение надо применить к числам a + n и
b + n, где n - натуральное число, такое что n ≥ a. Существование такого числа
следует из аксиомы Архимеда. ☻
Определение 1.4.6. Пусть дана последовательность отрезков числовой оси
{[ an; bn ]}, an < bn. Эту последовательность будем называть системой вло-
женных отрезков, если для любого n выполняются неравенства an ≤ an+1 и
bn+1 ≤ bn.
Для такой системы выполняются включения
[ a1; b1 ] ⊃ [ a2; b2 ] ⊃ [ a3; b3 ] ⊃... ⊃ [ an; bn ] ⊃...,
то есть каждый следующий отрезок содержится в предыдущем.
Теорема 1.4.4. Для всякой системы вложенных отрезков существует по
крайней мере одна точка, которая входит в каждый из этих отрезков.
►Возьмем два множества A = {an } и B = {bn }. Они не пусты и при любых
n и m выполняется неравенство an < bm. Докажем это.
Если n ≥ m, то an < bn ≤ bm. Если n < m, то an ≤ am < bm.
Таким образом, классы A и B удовлетворяют аксиоме непрерывности и,
следовательно, существует число λ такое, что an ≤ λ ≤ bn для любого n, т.е. это
число принадлежит любому отрезку [ an; bn ].◄
В дальнейшем (теорема 2.1.8) мы уточним эту теорему.
Утверждение, сформулированное в теореме 1.4.4, называется принципом
Кантора, а множество, удовлетворяющее этому условию, будем называть не-
прерывным по Кантору.
Мы доказали, что, если упорядоченное множество непрерывно по Деде-
кинду, то в нем выполнен принцип Архимеда и оно непрерывно по Кантору.
Можно доказать, что упорядоченное множество, в котором выполнены прин-
ципы Архимеда и Кантора, будет непрерывным по Дедекинду. Доказательство
этого факта содержится, например, в [4, том 1].
Принцип Архимеда позволяет каждому отрезку прямой сопоставить не-
которое единственное положительное число, удовлетворяющее условиям:
1. равным отрезкам соответствуют равные числа;
2. Если В точка отрезка АС и отрезкам АВ и ВС соответствуют числа a и
b, то отрезку АС соответствует число a + b;
3. некоторому отрезку соответствует число 1.
Число, соответствующее каждому отрезку и удовлетворяющее условиям 1-3 на-
зывается длиной этого отрезка.
Принцип Кантора позволяет доказать, что для каждого положительного
числа можно найти отрезок, длина которого равна этому числу. Таким образом,
между множеством положительных вещественных чисел и множеством отрез-
ков, которые откладываются от некоторой точки прямой по заданную сторону
от этой точки, можно установить взаимно однозначное соответствие.
Это позволяет дать определение числовой оси и ввести соответствие ме-
жду вещественными числами и точками на прямой. Для этого возьмем некото-
рую прямую и выберем на ней точку О, которая разделит эту прямую на два
луча. Один из этих лучей назовем положительным, а второй отрицатель-
ным. Тогда будем говорить, что мы выбрали направление на этой прямой.
Определение 1.4.7. Числовой осью будем называть прямую, на которой
заданы
а) точка О, называемая началом отсчета или началом координат;
б) направление;
в) отрезок единичной длины.
Теперь каждому вещественному числу a сопоставим точку M на число-
вой прямой таким образом, чтобы
а) числу 0 соответствовало начало координат;
б) OM = a - длина отрезка от начала координат до точки M равнялась
модулю числа;
в) если a - положительно, то точка берется на положительном луче и, ес-
ли оно отрицательно, то – на отрицательном.
Это правило устанавливает взаимно-однозначное соответствие между
множеством вещественных чисел и множеством точек на прямой.
Числовую прямую (ось) будем также называть вещественной прямой
(осью).
Отсюда также следует геометрический смысл модуля вещественного чис-
ла: модуль числа равен расстоянию от начала координат до точки, изобра-
жающей это число на числовой оси.
Теперь мы можем дать геометрическую интерпретацию свойствам 6 и 7
модуля вещественного числа. При положительном С числа x, удовлетворяю-
щие свойству 6, заполняют промежуток (−C, C), а числа x, удовлетворяющие
свойству 7, лежат на лучах (−∞,C) или (C, +∞).
Отметим еще одно замечательное геометрическое свойство модуля веще-
ственного числа.
Модуль разности двух чисел равен расстоянию между точками, соот-
ветствующими этим числам на вещественной оси.
Далее приведем обозначения, которые применяются для записи некото-
рых стандартных числовых множеств.
- множество натуральных чисел;
- множество целых чисел;
- множество рациональных чисел;
- множество вещественных чисел;
+, +, + - множества, соответственно, целых, рациональных и веще-
ственных неотрицательных чисел;
- множество комплексных чисел.
Кроме того, множество вещественных чисел обозначается как (−∞, +∞).
Подмножества этого множества:
(a, b) = { x | x ∈ R, a < x < b} - интервал;
[ a, b] = { x | x ∈ R, a ≤ x ≤ b} - отрезок;
(a, b] = { x | x ∈ R, a < x ≤ b} или [ a, b) = { x | x ∈ R, a ≤ x < b} - полуинтерва-
лы или полуотрезки;
(a, +∞) = { x | x ∈ R, a < x} или (−∞, b) = { x | x ∈ R, x < b} - открытые лучи;
[ a, +∞) = { x | x ∈ R, a ≤ x} или (−∞, b] = { x | x ∈ R, x ≤ b} - замкнутые лучи.
Наконец, иногда нам будут нужны промежутки, у которых нам не будет важно,
принадлежат его концы этому промежутку или нет. Такой промежуток будем
обозначать a, b.
§ 5 Ограниченность числовых множеств
Определение 1.5.1. Числовое множество X называется ограниченным
сверху, если существует число М такое, что x ≤ M для всякого элемента x из
множества X.
Определение 1.5.2. Числовое множество X называется ограниченным
снизу, если существует число m такое, что x ≥ m для всякого элемента x из
множества X.
Определение 1.5.3. Числовое множество X называется ограниченным,
если оно ограничено сверху и снизу.
В символической записи эти определения будут выглядеть следующим
образом:
множество X ограничено сверху, если ∃M ∀x ∈ X: x ≤ M,
ограничено снизу, если ∃m ∀x ∈ X: x ≥ m и
ограничено, если ∃m, M ∀x ∈ X: m ≤ x ≤ M.
Пустое множество будем считать ограниченным по определению.
Теорема 1.5.1. Числовое множество X ограничено тогда и только тогда,
когда существует число C такое, что для всех элементов x из этого множе-
ства выполняется неравенство x ≤ C.
► Пусть множество X ограничено. Положим C = max (m, M) - наи-
большее из чисел m и M. Тогда, используя свойства модуля вещественных
чисел, получим неравенства x ≤ M ≤ M ≤ C и x ≥ m ≥ − m ≥ −C, откуда следу-
ет, что x ≤ C.
Обратно, если выполняется неравенство x ≤ C, то −C ≤ x ≤ C. Это и есть тре-
буемое, если положить M = C и m = −C.◄
Число M, ограничивающее множество X сверху, называется верхней
границей множества. Если M - верхняя граница множества X, то любое
число M ′, которое больше M, тоже будет верхней границей этого множества.
Таким образом, мы можем говорить о множестве верхних границ множества
X. Обозначим множество верхних границ через M. Тогда, ∀x ∈ X и ∀M ∈ M
будет выполнено неравенство x ≤ M, следовательно, по аксиоме непрерывно-
сти существует число M 0 такое, что x ≤ M 0 ≤ M. Это число называется точ-
ной верхней границей числового множества X или верхней гранью этого
множества или супремумом множества X и обозначается M 0 = sup X.
Таким образом, мы доказали, что каждое непустое числовое множество,
ограниченное сверху, всегда имеет точную верхнюю границу.
Очевидно, что равенство M 0 = sup X равносильно двум условиям:
1) ∀x ∈ X выполняется неравенство x ≤ M 0, т.е. M 0 - верхняя граница множе-
ства X;
2) ∀ε > 0 ∃xε ∈ X так, что выполняется неравенство xε > M 0 − ε, т.е. эту гра-
ницу нельзя улучшить (уменьшить).
∞
⎧ 1⎫
Пример 1. Рассмотрим множество X = ⎨1 − ⎬. Докажем, что sup X = 1.
⎩ n ⎭n=1
☺Действительно, во-первых, неравенство 1 − < 1 выполняется для любого
n
n ∈; во-вторых, если взять произвольное положительное число ε, то по
принципу Архимеда можно найти натуральное число nε, такое что nε >. То-
ε
гда будет выполнено неравенство 1 − > 1 − ε, т.е. нашелся элемент xnε мно-
nε
жества X, больший чем 1 − ε, что означает, что 1 – наименьшая верхняя грани-
ца.☻
Аналогично, можно доказать, что если множество ограничено снизу, то
оно имеет точную нижнюю границу, которая называется также нижней гра-
нью или инфимумом множества X и обозначается inf X.
Равенство m0 = inf X равносильно условиям:
1) ∀x ∈ X выполняется неравенство x ≥ m0;
2) ∀ε > 0 ∃xε ∈ X так, что выполняется неравенство xε < m0 + ε.
Если в множестве X есть наибольший элемент x0, то будем называть его
максимальным элементом множества X и обозначать x0 = max X. Тогда
sup X = x0. Аналогично, если в множестве существует наименьший элемент, то
его будем называть минимальным, обозначать min X и он будет являться ин-
фимумом множества X.
Например, множество натуральных чисел имеет наименьший элемент –
единицу, который одновременно является и инфимумом множества. Супре-
мума это множество не имеет, так как оно не является ограниченным сверху.
Определения точных верхней и нижней границ можно распространить на
множества, неограниченные сверху или снизу, полагая, sup X = +∞ или, соот-
ветственно, inf X = −∞.
В заключение сформулируем несколько свойств верхних и нижних гра-
ней.
Свойство 1. Пусть X - некоторое числовое множество. Обозначим через
− X множество {− x | x ∈ X }. Тогда sup (− X) = − inf X и inf (− X) = − sup X.
Свойство 2. Пусть X - некоторое числовое множество λ - вещественное
число. Обозначим через λ X множество {λ x | x ∈ X }. Тогда если λ ≥ 0, то
sup (λ X) = λ sup X, inf (λ X) = λ inf X и, если λ < 0, то
sup (λ X) = λ inf X, inf (λ X) = λ sup X.
Свойство 3. Пусть X1 и X 2 - числовые множества. Обозначим через
X1 + X 2 множество { x1 + x2 | x1 ∈ X 1, x2 ∈ X 2 } и через X1 − X 2 множество
{ x1 − x2 | x1 ∈ X1, x2 ∈ X 2}. Тогда sup (X 1 + X 2) = sup X 1 + sup X 2,
inf (X1 + X 2) = inf X1 + inf X 2, sup (X 1 − X 2) = sup X 1 − inf X 2 и
inf (X1 − X 2) = inf X1 − sup X 2.
Свойство 4. Пусть X1 и X 2 - числовые множества, все элементы кото-
рых неотрицательны. Тогда
sup (X1 X 2) = sup X1 ⋅ sup X 2, inf (X1 X 2) = inf X 1 ⋅ inf X 2.
Докажем, например, первое равенство в свойстве 3.
►Пусть x1 ∈ X1, x2 ∈ X 2 и x = x1 + x2. Тогда x1 ≤ sup X1, x2 ≤ sup X 2 и
x ≤ sup X1 + sup X 2, откуда sup (X1 + X 2) ≤ sup X1 + sup X 2.
Чтобы доказать противоположное неравенство, возьмем число
* *
y < sup X 1 + sup X 2. Тогда можно найти элементы x1 ∈ X1 и x2 ∈ X 2 такие,
* *
что x1 < sup X1 и x2 < sup X 2, и выполняется неравенство
* *
y < x1 + x2 < sup X1 + sup X 2. Это означает, что существует элемент
* * *
x = +x1 x2 ∈ X1+ X2, который больше числа y и
sup X1 + sup X 2 = sup (X1 + X 2).◄
Доказательства остальных свойств проводятся аналогично и предостав-
ляются читателю.
§ 6 Счетные и несчетные множества
Определение 1.6.1. Рассмотрим множество первых n натуральных чисел
n = {1,2,..., n} и некоторое множество A. Если можно установить взаимно-
однозначное соответствие между A и n, то множество A будем называть
конечным.
Определение 1.6.2. Пусть дано некоторое множество A. Если можно
установить взаимно однозначное соответствие между множеством A и
множеством натуральных чисел, то множество A будем называть счет-
ным.
Определение 1.6.3. Если множество A конечно или счетно, то будем го-
ворить, что оно не более чем счетно.
Таким образом, множество будет счетно, если его элементы можно рас-
положить в виде последовательности.
Пример 1. Множество четных чисел – счетное, так как отображение n ↔ 2n
является взаимно однозначным соответствием между множеством натуральных
чисел и множеством четных чисел.
Очевидно, такое соответствие можно установить не единственным обра-
зом. Например, можно установить соответствие между множеством и мно-
жеством (целых чисел), установив соответствие таким способом
 2015-10-16
2015-10-16 22435
22435