Наряду с понятиями множества и элемента в математике первичным понятием является понятие соответствия. Это понятие неявным образом присутствует и в понятии множества, поскольку понятие множества предполагает, что каждый элемент данного множества обладает определенным свойством, отличающим его от элементов, не входящих в это множество. Иначе говоря, каждому из рассматриваемых элементов поставлено в соответствие некоторое свойство, позволяющее судить о том, является этот элемент элементом данного множества или нет.
Среди всевозможных соответствий важную роль в математике играют соответствия, называемые функциями. Опишем эти соответствия.
Пусть заданы непустые множества X и Y. Соответствие, при котором каждому элементу x  X соответствует единственный элемент y
X соответствует единственный элемент y  Y, называется функцией, заданной (определенной) на множестве X со значениями в множестве Y, или отображением множества X в множество Y. Такая функция (такое отображение) обозначается с помощью некоторой буквы, например, буквы f одним из следующих способов:
Y, называется функцией, заданной (определенной) на множестве X со значениями в множестве Y, или отображением множества X в множество Y. Такая функция (такое отображение) обозначается с помощью некоторой буквы, например, буквы f одним из следующих способов:
y = f(x), x  X, или f: X
X, или f: X 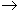 Y или f: x
Y или f: x 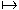 y, x
y, x  X, y
X, y  Y.
Y.
Наряду с терминами "функция", "отображение" употребляются равнозначные термины "преобразование", "морфизм". Элемент x  X называется независимым переменным или аргументом, а соответствующий элемент y
X называется независимым переменным или аргументом, а соответствующий элемент y  Y - зависимым переменным. Множество X называется множеством задания (определения) функции f, а множество тех y
Y - зависимым переменным. Множество X называется множеством задания (определения) функции f, а множество тех y  Y, каждый из которых поставлен в соответствие хотя бы одному x
Y, каждый из которых поставлен в соответствие хотя бы одному x  X - множеством значений функции f и обозначается Yf. Очевидно, Yf
X - множеством значений функции f и обозначается Yf. Очевидно, Yf 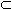 Y. Если Yf =Y, то отображение f называется отображением X на множество Y или сюръекцией. Если при x
Y. Если Yf =Y, то отображение f называется отображением X на множество Y или сюръекцией. Если при x 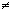 x выполняется неравенство f (x)
x выполняется неравенство f (x) 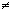 f (x'), то отображение f называется взаимно однозначным отображением X в Y или инъекцией. Если f является взаимно однозначным отображением X на Y, т.е. является одновременно сюръекцией и инъекцией, то оно называется биекцией.
f (x'), то отображение f называется взаимно однозначным отображением X в Y или инъекцией. Если f является взаимно однозначным отображением X на Y, т.е. является одновременно сюръекцией и инъекцией, то оно называется биекцией.
Если задано отображение f: X 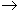 Y, то элементы множеств X и Y часто называются точками.
Y, то элементы множеств X и Y часто называются точками.
Символом f (x) обозначается как сама функция, так и элемент, соответствующий элементу x при этой функции. Обозначение одним и тем же символом f (x) как самой функции, так и ее значения в точке x не приводит к недоразумениям, так как всегда из контекста ясно, о чем идет речь. Значение функции в точке xo обозначается также f (x)|xo.
Если f: X-> Y и E - подмножество множества X, то функция fE: X-> Y, такая, что для каждого x  E выполняется равенство fE (x)= f (x), называется сужением функции на множество E. Таким образом, сужение fE функции f принимает в точках x множества E те же значения, что и функция f. Иногда сужение fE функции f обозначают тем же символом f, что и саму исходную функцию, и называют функцией f на множестве E.
E выполняется равенство fE (x)= f (x), называется сужением функции на множество E. Таким образом, сужение fE функции f принимает в точках x множества E те же значения, что и функция f. Иногда сужение fE функции f обозначают тем же символом f, что и саму исходную функцию, и называют функцией f на множестве E.
Пусть заданы функция f: X 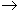 Y и A
Y и A 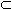 X. Множество всех y
X. Множество всех y  Y, являющихся значениями функции f в точках x
Y, являющихся значениями функции f в точках x  А, называется образом множества A при отображении f и обозначается f (A), т. е.
А, называется образом множества A при отображении f и обозначается f (A), т. е.
f (A)  { y: { y: 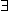 x x  A, f (x)= y }. A, f (x)= y }. |
В частности, образ множества X есть множество значений функции: f (X) = Yf. Если B 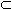 Y, то множество всех тех точек x
Y, то множество всех тех точек x  X, значения функции f в которых принадлежат множеству B, называется прообразом множества B. То есть прообразом множества B является множество { x: f (x)
X, значения функции f в которых принадлежат множеству B, называется прообразом множества B. То есть прообразом множества B является множество { x: f (x)  B }.
B }.
Пусть Z - некоторое множество и Y = 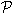 (Z) - множество всех его подмножеств. Если f: X
(Z) - множество всех его подмножеств. Если f: X 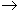 Y, то значение f (x) функции f в точке x
Y, то значение f (x) функции f в точке x  X является в этом случае некоторым подмножеством множества Z: f (x)
X является в этом случае некоторым подмножеством множества Z: f (x) 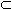 Z. Если среди подмножеств f (x), x
Z. Если среди подмножеств f (x), x  X, имеется по крайней мере одно непустое множество, содержащее более одного элемента, то функция f называется многозначной функцией. При этом всякий элемент z
X, имеется по крайней мере одно непустое множество, содержащее более одного элемента, то функция f называется многозначной функцией. При этом всякий элемент z  Z, принадлежащий множеству f (x)
Z, принадлежащий множеству f (x) 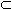 Z, т.е. z
Z, т.е. z  f (x), часто также называется значением функции f в точке x
f (x), часто также называется значением функции f в точке x  X.
X.
Если каждое из множеств f (x) состоит только из одного элемента, то функцию f называют однозначной функцией. Пусть 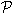 (X)- множество всех подмножеств множества X. Функция, определенная на множестве Yf = f (X) значений функции f: X (X)- множество всех подмножеств множества X. Функция, определенная на множестве Yf = f (X) значений функции f: X 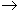 Y, с областью значений, принадлежащей множеству Y, с областью значений, принадлежащей множеству 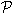 (X), и ставящая в соответствие каждому элементу y (X), и ставящая в соответствие каждому элементу y  Yf его прообраз { x: f (x)= y }, называется обратной к f функцией и обозначается через f -1: Yf Yf его прообраз { x: f (x)= y }, называется обратной к f функцией и обозначается через f -1: Yf 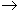 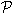 (X). Обратная функция является, вообще говоря, многозначной функцией. Если отображение взаимно однозначно (т.е. является инъекцией), то обратная функция является однозначной. Если отображение f является взаимно однозначным отображением X на Y, то обратное отображение f -1 является взаимно однозначным отображением Y на X (т. е. если f: X (X). Обратная функция является, вообще говоря, многозначной функцией. Если отображение взаимно однозначно (т.е. является инъекцией), то обратная функция является однозначной. Если отображение f является взаимно однозначным отображением X на Y, то обратное отображение f -1 является взаимно однозначным отображением Y на X (т. е. если f: X 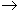 Y - биекция, то и f -1: Y Y - биекция, то и f -1: Y  X - биекция), и поэтому f является в свою очередь отображением, обратным к отображению f -1. Это означает, что при любом x X - биекция), и поэтому f является в свою очередь отображением, обратным к отображению f -1. Это означает, что при любом x  X имеет место равенство f -1 f (x)= x, а при любом y X имеет место равенство f -1 f (x)= x, а при любом y  f (X) - равенство f f -1(y)= y. При этом для заданного инъективного отображения f: X f (X) - равенство f f -1(y)= y. При этом для заданного инъективного отображения f: X  Y каждое из указанных двух условий однозначно определяет обратное отображение f -1. Если f: X Y каждое из указанных двух условий однозначно определяет обратное отображение f -1. Если f: X  Y и g: Y Y и g: Y  Z, то функция F: X Z, то функция F: X  Z, ставящая в соответствие каждому элементу x Z, ставящая в соответствие каждому элементу x  X элемент F (x)= g (f (x)), называется композицией функций f и g (иногда – суперпозицией этих функций или сложной функцией) и обозначается g X элемент F (x)= g (f (x)), называется композицией функций f и g (иногда – суперпозицией этих функций или сложной функцией) и обозначается g  f. Таким образом, согласно определению для каждого x f. Таким образом, согласно определению для каждого x  X имеет место равенство (g X имеет место равенство (g  f)(x) f)(x)  g (f (x)). g (f (x)). |
Счетные множества. Множества Е и F называются равномощными если существует биекция f: E -> F. Множество E называется счетным, если оно равномощно множеству натуральных чисел N.
Пример. Множество рациональных чисел Q счетно. Доказательство.
Представим рациональные числа в виде следующей таблицы:
0 1/1 1/2 1/3 1/4…
-1/1 -1/2 -1/3 -1/4…
2/1 2/2 2/3…
-2/1 -2/2 -2/3…
3/1 3/2…
-3/1 -3/2…
4/1…
-4/1…
Искомая биекция будет f: N->Q может быть определена правилом:
f(1)=0, f(2)=1/1, f(3)=-1/1, f(4)=1/2, f(5)=-1/2, ….
(встречающиеся ранее числа в дальнейшей нумерации не участвуют). Таким образом, Q равномощно N.
 2015-10-16
2015-10-16 1175
1175
