Лекция 4. Эквивалентные формулировки свойства непрерывности

4.1. Существование иррациональных чисел. Возникает вопрос, что, может быть, рациональные числа исчерпывают все элементы множества R? Ответ на этот вопрос дает аксиома непрерывности. Действительно, для рациональных чисел эта аксиома не выполняется. Для примера, рассмотрим два множества:

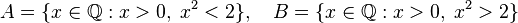
Легко видеть, что для любых элементов 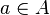и 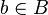выполняется неравенство 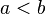. Однако рационального числа 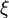, разделяющего эти два множества, не существует. В самом деле, этим числом может быть только 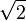, но оно не является рациональным. Этот факт и указывает на то, что существуют иррациональные числа в множестве R.

Кроме четырех арифметических действий над числами можно производить действия возведения в степень и извлечения корня. Для любого числа 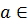R и натурального n степень aⁿ определяется как произведение n сомножителей, равных a: 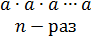= 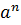. По определению a⁰ 1, a >0, a ^-n 1/ a ⁿ, a 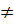0, n - натуральное число.

Пусть a >0, n - натуральное число. Число b называется корнем n -й степени из числа a, если bⁿ=a. В этом случае пишется 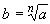. Существование и единственность положительного корня любой степени n из любого положительного числа будет доказано ниже.

Пример 4.1.1. Неравенство Бернулли: (1+x)ⁿ > 1+nx ( Доказать методом индукции самостоятельно).