Лекция 1. Множества и операции над ними.
Введение. Без преувеличения можно сказать, что «Математический анализ» составляет основу математического образования. Название курса «Математический анализ» представляет собой сокращенное видоизменение старого названия «Анализа посредством бесконечно малых». Что же анализируют с помощью бесконечно малых? В классическом математическом анализе такими объектами являются прежде всего функции, те есть переменные величины, зависящие от других переменных величин. Ближайшая наша задача – изучение достаточно общих, встречающихся на практике, функций методами бесконечно малых или, что то же самое, методами пределов. Сущность этого метода постепенно будет раскрыта в процессе данного курса. Определение понятия функции основывается на понятие множества, поэтому прежде всего познакомимся кратко с теорией множеств.
Множества.
Основоположником теории множеств, принято считать Георга Кантора (1845-1918гг) – известного немецкого математика. Что же такое множество и как его определить? В математике очень часто встречаются понятия, которые трудно строго определить, а часто даже невозможно. Например, какое строгое определение можно дать точке на плоскости или прямой? Думаю, что это сделать просто невозможно - это интуитивные понятия. Вот и множество относится к таким понятиям. Георгий Кант так определял это понятие «Множество есть многое, мыслимое как единое целое». Но это опять не строгое определение, так как появляется слово многое – синоним множества.
Постараемся все-таки пояснить, что мы будем понимать под множеством. Сформулируем следующее отношение: «Вещи a,b,c,… особым, не подлежащим определению образом, определяют вещь М и, обратно, вещь М определяет вещи a,b,c,…». Это отношение мы будем выражать словами: «Множество М состоит из объектов a,b,c,…». Таким образом, множество считается заданным, если про всякую вещь определено, входит она в это множество или нет.
Множества бывают конечными и бесконечными. Например, множества сторон многоугольника, множество корней некоторого многочлена – это конечные множества, а множество натуральных чисел, множество точек отрезка – бесконечные множества.
Введем некоторые обозначения. Большими буквами, как правило, будем обозначать множества: A, B, C, X, Y,..., а малыми - их элементы: a, b, c, x, y,... и т. д. Запись A ={ a, b, c,...} означает, что множество A состоит из элементов a, b, c,..., а запись A ={ x: условие} или A ={ x | условие} означает, что множество A состоит из всех таких элементов x, которые удовлетворяют условию, написанному после двоеточия или, соответственно, после вертикальной черты (двоеточие и вертикальная черта в этом случае читаются как "таких что"). Через a  A обозначается принадлежность элемента a множеству A, а a
A обозначается принадлежность элемента a множеству A, а a 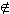 A означает, что элемент a не принадлежит множеству A. Для удобства вводится понятие пустого множества, которое обозначается символом
A означает, что элемент a не принадлежит множеству A. Для удобства вводится понятие пустого множества, которое обозначается символом 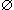 . Пустое множество не содержит элементов. Символы A
. Пустое множество не содержит элементов. Символы A 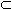 B и A
B и A 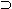 B выражают собой включение множества A в множество B. В этом случае множество A называется подмножеством множества B. В частности, здесь возможен случай A = B. Если A
B выражают собой включение множества A в множество B. В этом случае множество A называется подмножеством множества B. В частности, здесь возможен случай A = B. Если A 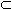 B и A
B и A 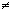 B, то A называется собственным подмножеством множества B.
B, то A называется собственным подмножеством множества B.
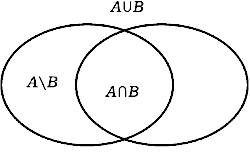 Рис. 1. Диаграмма Эйлера - Венна Рис. 1. Диаграмма Эйлера - Венна |
Символом A  B обозначается объединение множеств A и B; т. е. множество всех элементов, каждый из которых принадлежит хотя бы одному из множеств A и B, символом A
B обозначается объединение множеств A и B; т. е. множество всех элементов, каждый из которых принадлежит хотя бы одному из множеств A и B, символом A  B – пересечение множеств A и B, т. е. множество всех элементов, принадлежащих одновременно A и B; символом A \ B – разность множеств A и B, т. е. множество всех элементов, принадлежащих множеству A, но не принадлежащих множеству B (рис.1). В случае семейства множеств {
B – пересечение множеств A и B, т. е. множество всех элементов, принадлежащих одновременно A и B; символом A \ B – разность множеств A и B, т. е. множество всех элементов, принадлежащих множеству A, но не принадлежащих множеству B (рис.1). В случае семейства множеств { 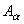 },
}, 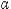

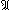 , где
, где 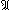 - некоторое множество индексов
- некоторое множество индексов 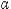 , символом
, символом 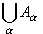 обозначается объединение всех множеств
обозначается объединение всех множеств 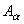 ,
, 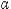

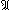 , а символом
, а символом 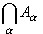 - их пересечение. Вместо слов "существует", "найдется", "имеется" в логических формулах употребляется символ
- их пересечение. Вместо слов "существует", "найдется", "имеется" в логических формулах употребляется символ 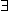 (перевернутая первая буква английского слова exist - существовать), называемый символом существования, а вместо слов "любой", "каждый", "произвольный", "какой бы ни" - символ
(перевернутая первая буква английского слова exist - существовать), называемый символом существования, а вместо слов "любой", "каждый", "произвольный", "какой бы ни" - символ 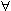 (перевернутая первая буква английского слова all - "все"), называемый символом всеобщности. Так, запись
(перевернутая первая буква английского слова all - "все"), называемый символом всеобщности. Так, запись 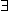 x читается "существует x ", а запись
x читается "существует x ", а запись 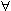 x - "любое x " или "для любого x " или "для всех x ". Соответственно запись
x - "любое x " или "для любого x " или "для всех x ". Соответственно запись 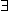 x,
x, 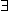 y, или, короче,
y, или, короче, 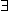 x,y означает "существуют x и y ", а запись
x,y означает "существуют x и y ", а запись 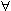 x,
x, 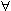 y, или, короче,
y, или, короче, 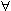 x, y - "любые x и y " или "для любых x и y ". Знак
x, y - "любые x и y " или "для любых x и y ". Знак 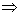 означает "следует", "вытекает", а знак
означает "следует", "вытекает", а знак 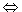 - "равносильно". В этих обозначениях формула A
- "равносильно". В этих обозначениях формула A 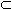 B
B 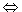 (x
(x  A
A 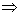 x
x  B) означает, что утверждение "множество A является подмножеством множества B " равносильно утверждению "из того, что элемент x принадлежит множеству A, следует, что он принадлежит множеству B ". Символ
B) означает, что утверждение "множество A является подмножеством множества B " равносильно утверждению "из того, что элемент x принадлежит множеству A, следует, что он принадлежит множеству B ". Символ  означает определение выражения, стоящего слева от этого символа (def - первые три буквы английского слова definition, что означает "определение"). Например, определение объединения
означает определение выражения, стоящего слева от этого символа (def - первые три буквы английского слова definition, что означает "определение"). Например, определение объединения 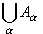 и пересечения
и пересечения 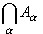 системы множеств {
системы множеств { 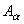 } можно записать в виде формул следующим образом:
} можно записать в виде формул следующим образом:
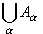
 { x:
{ x: 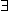
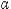 , x
, x 
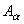 },
}, 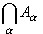
 { x:
{ x: 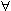
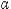 , x
, x 
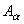 }.
}.
Определение часто используемого в математике символа 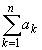 для обозначения суммы слагаемых ak можно записать следующим образом:
для обозначения суммы слагаемых ak можно записать следующим образом:
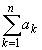  a 1 + a 2 +... +ak. a 1 + a 2 +... +ak. |
Всякому подмножеству X множества E сопоставим подмножество CX, состоящее из всех элементов E, которые не принадлежат X. CX называется дополнением множества X.
Операции объединения и пересечения множеств обладают свойством коммутативности и ассоциативности, то есть
1. XUY=YUX, X 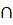 Y=Y
Y=Y 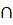 X (Коммутативность)
X (Коммутативность)
2. (XUY)UZ=XU(YUZ), (X 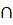 Y)
Y) 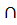 Z=X
Z=X 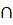 (Y
(Y 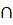 Z) (Ассоциативность).
Z) (Ассоциативность).
Эти свойства вытекают из определения рассматриваемых операций. Кроме того, эти две операции связаны соотношением дистрибутивности:
1. (XUY) 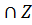 =(X
=(X 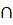 Z)U(Y
Z)U(Y 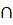 Z).
Z).
2. (X 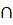 Y)UZ=(XUZ)
Y)UZ=(XUZ) 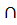 (YUZ).
(YUZ).
Доказательство.
Возьмем произвольный элемент x из множества (XUY) 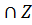 =>
=> 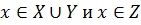 , так как
, так как 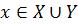 , то
, то 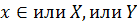 . Пусть
. Пусть 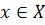 , тогда, очевидно,
, тогда, очевидно, 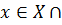 Z и следовательно
Z и следовательно 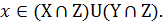 Аналогично если
Аналогично если 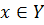 . Таким образом мы показали, что левая часть включается в правую. Совершенно также доказывается включение правой части равенства в – левую часть. Второе свойство доказывается аналогично.
. Таким образом мы показали, что левая часть включается в правую. Совершенно также доказывается включение правой части равенства в – левую часть. Второе свойство доказывается аналогично.
 2015-10-16
2015-10-16 1220
1220