Лекция 6. Числовая прямая

6.1. Доказательство существования и единственности решения уравнения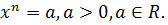

Пусть X множество таких чисел x из R, что 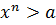. Множество всех остальных чисел из R обозначим Y. Очевидно, что 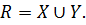По принципу Архимеда найдутся такие натуральные числа m и k, что 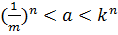. Таким образом, множества X и Y не пусты. Кроме того, x>0 и 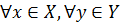выполняется неравенство x>y. Следовательно, можно говорить, что множества X и Y образуют сечение R. По принципу Дедекинда существует единственное число 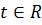, производящее это сечение. Допустим, что 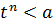, то есть 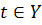, а значит, является наибольшим числом этого множества. Возьмем число h такое, что 0<h<1 и рассмотрим выражение

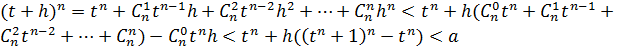, где .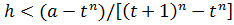

Отсюда следует, что t+h – элемент множества Y, что противоречит тому, что t – наибольший элемент множества Y. Пусть теперь 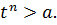Это означает, что t принадлежит множеству X и является наименьшим числом в этом множестве. Тогда

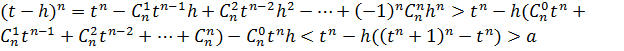, где .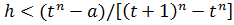

Следовательно, t-h 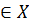, что противоречит тому, что t есть наименьший элемент множества X. Таким образом, остается единственная возможность 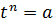ч.т.д.

Можно дать иное доказательство (конструктивное) сформулированного выше утверждения о существовании корня n – ой степени из a.

Рассмотрим последовательность действительных чисел вида:

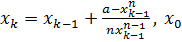-любое число такое, что 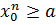. По индукции нетрудно показать, что 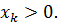Кроме того, так как a>0 и 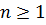, то 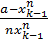>-1 и к выражению 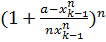можно применить неравенство Бернулли. Следовательно, можно записать

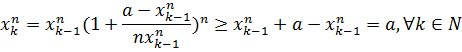
Это означает, что последовательность 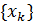ограничена с низу. Более того

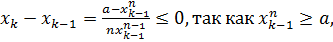то есть заданная последовательность монотонно убывает. Поэтому по теореме Вейерштрасса она имеет предел. Обозначим его 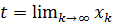. Переходя к пределу в формуле, определяющей заданную последовательность, получаем 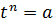. Если предположить, что существуют два решения 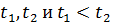, то отсюда будет следовать, что a<a чего быть не может.

Этот метод доказательства полезен тем, что позволяет вычислять корень n -степени из любого положительного числа. Действительно, пусть n=3, a=5, 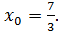Тогда 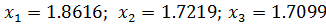…Третий член последовательности совпадает с точным решением до четвертого знака после запятой.