Существование верхней (нижней) грани

Докажем еще одну теорему, которая опирается на свойство непрерывности действительных чисел.

Терема о существовании верхней (нижней) грани. Сначала введем несколько определений.

Определение. Числовое множество X называется ограниченным сверху, если существует число М такое, что x ≤ M для всякого элемента x из множества X.

Определение. Числовое множество X называется ограниченным снизу, если существует число m такое, что x ≥ m для всякого элемента x из множества X.

Определение. Числовое множество X называется ограниченным, если оно ограничено сверху и снизу.

В символической записи эти определения будут выглядеть следующим образом:

множество X ограничено сверху, если ∃M ∀x ∈ X: x ≤ M,

ограничено снизу, если ∃m ∀x ∈ X: x ≥ m и

ограничено, если ∃m, M ∀x ∈ X: m ≤ x ≤ M.

Пустое множество будем считать ограниченным по определению.

Определение. Для любого числа a R неотрицательное число

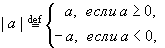
называется его абсолютной величиной или модулем. Для абсолютных величин чисел справедливо неравенство |a+b| < |a|, которое вытекает из определения модуля числа и из аксиом сложения и порядка.

Теорема 4.3.1. Числовое множество X ограничено тогда и только тогда, когда существует число C такое, что для всех элементов x из этого множества выполняется неравенство 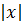≤ C.

Доказательство.► Пусть множество X ограничено. Положим C =max(m, M) - наибольшее из чисел m и M. Тогда, используя свойства модуля вещественных чисел, получим неравенства x ≤M≤M ≤C и x≥m≥ −m≥ −C, откуда следует, что 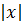≤ C.

Обратно, если выполняется неравенство 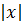≤ C, то −C ≤ x ≤ C. Это и есть требуемое, если положить M = C и m = −C.◄

Число M, ограничивающее множество X сверху, называется верхней границей множества. Если M - верхняя граница множества X, то любое число M′, которое больше M, тоже будет верхней границей этого множества. Таким образом, мы можем говорить о множестве верхних границ множества X. Обозначим множество верхних границ через 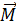. Тогда, ∀x ∈ X и ∀M ∈ 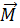будет выполнено неравенство x ≤M, следовательно, по аксиоме непрерывности существует число 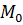такое, что x ≤ 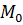≤ M. Это число называется точной верхней границей числового множества X или верхней гранью этого множества или супремумом множества X и обозначается 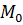=sup X. Таким образом, мы доказали, что каждое непустое числовое множество, ограниченное сверху, всегда имеет точную верхнюю границу.

Очевидно, что равенство 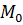= sup X равносильно двум условиям:

1) ∀x ∈ X выполняется неравенство x ≤ 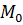, т.е. 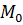- верхняя граница множества X;

2) ∀ε > 0 ∃xε ∈ X так, что выполняется неравенство xε > 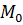−ε, т.е. эту границу нельзя улучшить (уменьшить).

Аналогично, можно доказать, что если множество ограничено снизу, то оно имеет точную нижнюю границу, которая называется также нижней гранью или инфимумом множества X и обозначается inf X. Равенство 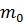=inf X равносильно условиям:

1) ∀x ∈ X выполняется неравенство x ≥ ;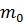

2) ∀ε > 0 ∃xε ∈ X так, что выполняется неравенство x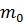ε < + ε.

Если в множестве X есть наибольший элемент 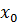, то будем называть его

максимальным элементом множества X и обозначать 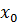= max X. Тогда

supX = 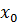. Аналогично, если в множестве существует наименьший элемент, то его будем называть минимальным, обозначать minX и он будет являться инфимумом множества X.

Cформулируем несколько свойств верхних и нижних граней:

Свойство 1. Пусть X - некоторое числовое множество. Обозначим через −X множество {− x| x ∈ X }. Тогда sup (− X) = − inf X и inf (− X) = − sup X.

Свойство 2. Пусть X - некоторое числовое множество λ – вещественное число. Обозначим через λX множество {λx | x ∈ X }. Тогда если λ ≥ 0, то sup(λX) = λ supX, inf(λ X)= λ infX и, если λ < 0, то sup(λ X)=λ infX, inf(λ X)=λ supX.

Свойство 3. Пусть X1 и X2 - числовые множества. Обозначим через X1+X2 множество { x1+ x2| x1 ∈ X1, x2 ∈ X2 } и через X1 − X2 множество {x1 − x2 | x1 ∈ X1, x2 ∈ X2}. Тогда sup(X1 + X2)=supX1+supX2, inf(X1+X2)=infX1 +inf X2, sup(X1 − X2) = sup X1 − inf X2 и inf (X1 − X2) = inf X1 − sup X2.

Свойство 4. Пусть X1 и X2 - числовые множества, все элементы которых неотрицательны. Тогда sup (X1*X2) = sup X1 *sup X2, inf (X1*X2) = inf X1* inf X2.

Докажем например первое равенство свойства 3. Пусть x1 ∈ X1, x2 ∈ X2 и x=x1+x2. Тогда x1 ≤ sup X1, x2 ≤ sup X2 и x ≤ sup X1 + sup X2, откуда sup(X1 + X2) ≤ sup X1 + sup X2.

Чтобы доказать противоположное неравенство, возьмем число y<supX1+supX2. Тогда можно найти элементы 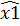∈ X1 и 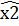∈ X2 такие, что 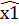<sup X1 и 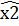<sup X2, и выполняется неравенство y<x1+x2<supX1+supX2. Это означает, что существует элемент 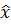= 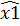+ 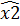∈ X1+X2, который больше числа y и sup X1 + sup X2 = sup (X1 + X2). Остальные соотношения доказываются аналогично.

Принцип Архимеда и существование верхней и нижней граней можно постулировать как аксиому вместо аксиомы непрерывности, тогда аксиома непрерывности будет следовать из этой новой аксиомы. (Попробуйте доказать самостоятельно).