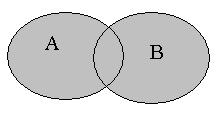
 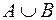 Рис. 2.2. Рис. 2.2. | Суммой или объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком 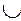 . . |
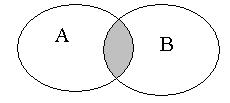 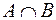 Рис. 2.3. Рис. 2.3. | Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. Эта операция над множествами обозначается знаком 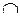 . Если . Если 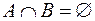 , то множества , то множества 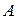 и и 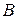 называются непересекающимися. называются непересекающимися. |
Два множества называются непересекающимися (или расчлененными) если 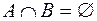 . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества
. Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества 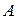 называется такая расчлененная система непустых подмножеств множества
называется такая расчлененная система непустых подмножеств множества 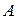 , что каждый элемент множества
, что каждый элемент множества 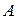 является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
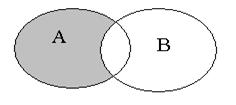 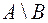 Рис. 2.4. Рис. 2.4. | Разностью множеств 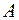 и и 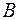 или дополнением или дополнением 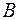 до до 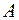 называется множество, состоящее только из тех элементов называется множество, состоящее только из тех элементов 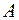 , которые не входят в , которые не входят в 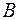 . Эта операция над множествами обозначается знаком . Эта операция над множествами обозначается знаком 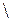 . . |
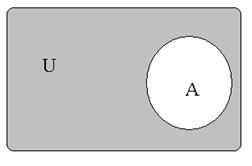 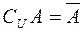 Рис. 2.5. Рис. 2.5. | Часто все рассматриваемые множества считают подмножествами одного основного множества 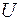 . В таком случае разность . В таком случае разность 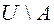 (дополнение (дополнение 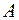 до до 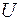 ) обозначают, как ) обозначают, как 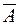 , а операцию называют взятием дополнения. , а операцию называют взятием дополнения. |
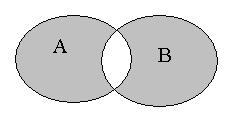 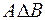 Рис. 2.6. Рис. 2.6. | Симметрической разностью множеств 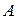 и и 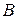 называется множество называется множество 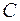 : : 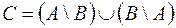 . Обозначается симметрическая разность: . Обозначается симметрическая разность: 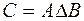 или или 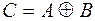 . . |
Для подмножеств данного множества 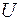 выполняются следующие законы:
выполняются следующие законы:
· Закон коммутативности (переместительный закон):
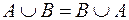 ;
; 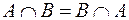 ;
;
· Закон ассоциативности (сочетательный закон) для любой тройки множеств 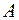 ,
, 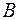 и
и 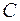 :
:
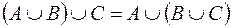 ;
;
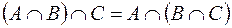 ;
;
· Закон дистрибутивности (распределительный закон) для любой тройки множеств 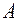 ,
, 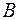 и
и 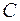 :
:
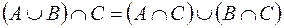 ;
;
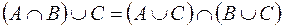 ;
;
· 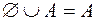 ;
; 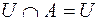 ;
;
· 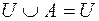 ;
; 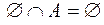 ;
;
· 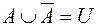 ;
; 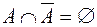 ;
;
· 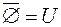 ;
;
· 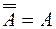 ;
;
· 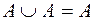 ;
; 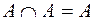 ;
;
· 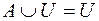 ;
; 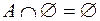 ;
;
· 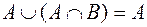 ;
; 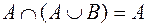 ;
;
· 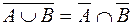 ;
; 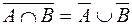 .
.
Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения множеств – операцию умножения, универсальному множеству 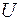 – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
– единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой 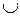 на
на 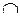 ,
, 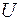 на
на 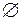 и наоборот. Такие выражения называются двойственными друг другу.
и наоборот. Такие выражения называются двойственными друг другу.
Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством.
Очевидно, что операция разность не обладает свойствами коммутативности и ассоциативности, в то же время операция симметрическая разность и коммутативна, и ассоциативна.
Большое значение в современной математике имеет множественная операция декартово произведение. Если заданы два множества 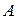 и
и 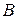 , то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств
, то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств 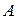 и
и 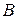 называется множество
называется множество 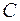 , составленное из упорядоченных пар (
, составленное из упорядоченных пар (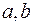 ). Декартово произведение множеств
). Декартово произведение множеств 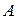 и
и 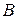 обозначается
обозначается 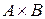 .
.
Очевидно, что 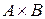 и
и 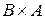 ‑ различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
‑ различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
 2015-10-13
2015-10-13 1990
1990
