1. По определению 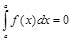 .
.
2. По определению 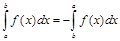 .
.
3. Каковы бы ни были числа a, b, c, всегда имеет место равенство
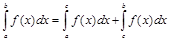 .
.
4. Постоянный множитель можно выносить за знак определённого интеграла, т. е.
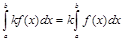 .
.
5. Определённый интеграл от алгебраической суммы функции равен алгебраической сумме их интегралов, т. е.
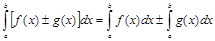 .
.
Формула Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке [a;b] и F(x) есть какая-либо первообразная для f(x) на этом отрезке, то справедлива следующая формула:
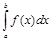 =F(b)-F(a). (2)
=F(b)-F(a). (2)
Пример 1. Вычислить: 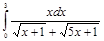 .
.
Решение: применим формулу Ньютона-Лейбница:
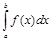 =F(x)|
=F(x)|  =F(b) - F(a)
=F(b) - F(a)
Преобразуем подынтегральную функцию
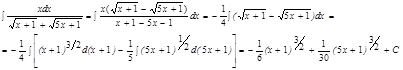 .
. 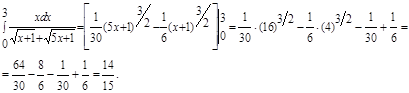
 2015-10-13
2015-10-13 388
388








