Тема 24. Логика как основа философского мировоззрения

1. История и предмет логики.

2. Логика и язык.

3. Логический анализ понятий и основных законов логики.

История и предмет логики

Термин «логика» произошел от древнегреческого слова «logos» (мысль, слово, учение). В античной философии это понятие обозначало разумный принцип, управляющий миром. В современной научной литературе термин «логика» употребляют в следующих значениях:

1) в значении необходимой, закономерной связи в объективном мире, когда речь идет «о логике событий», «о логике вещей», «о логике исторического процесса» и т.п.;

2) в значении закономерного характера наших мыслей, когда речь идет «о логике рассуждений», «о логике изложения статьи или лекции», «о логике теории» и т.д.

3) в значении логики наших действий и тогда мы говорим, что «его деятельность логически последовательна» или «его поступки нелогичны»;

4) логикой называют науку как определенную систему знаний о формах и законах правильного мышления.

Логика зародилась и развивалась в рамках философии и, при решении собственно философских проблем, выступала в качестве метода рационального обоснования своих позиций в борьбе против религиозно – мифологического мировоззрения.

В историческом развитии логики выделяется два больших периода, обусловленных изменением содержания, структуры и методов логических исследований. Первый период: от зарождения логики и до рубежа XIX – XX вв. Второй период: от рубежа XIX – XX вв. до настоящего времени. Очертим круг проблем, которые решались в эти периоды.

Первые логические учения появились в Древней Индии, Древнем Китае и Древней Греции. Логические учения в Древней Индии появились в VI в. до н.э. и были тесно связаны с религиозно – философскими учениями буддизма и джайнизма. Начиная с IV в. до н.э. формируются семь ортодоксальных философских школ. Многочисленные дискуссии между сторонниками этих школ, способствовали дальнейшему развитию логики и теории познания.

Особенностью буддийской логики является разработка многочисленного силлогизма с пятью и более элементами. Известный востоковед, индолог Д.И.Щербатский определял буддийскую логику как систему логики и эпистемологии, созданную в Индии в VI – VII вв. мыслителями Васубандху (410/420 – 490/500), Дигнага (V – VI вв.), Дхармакирти (VII в.).

Древнекитайская логика начинает развиваться с V в. до н.э. в сочинениях основателя философской школы моистов Мо Ди (Мо - Цзы) (468-376 до н.э.). Моисты разрабатывали систему логических доказательств, с помощью которых устанавливали соотношения объема и содержания понятий, занимались классификацией имен, разработали семь методов рассуждения.

В европейской культуре логика как самостоятельная наука возникла в Древней Греции в IV в. до н.э. Ее основателем является Аристотель (384 – 322 до н.э.). Аристотель создает дедуктивную логику и определяет ее как науку о доказательстве и средствах обоснования истины.

В средние века логика продолжает разрабатываться в рамках схоластической философии. В философии Нового времени существенный вклад в развитие логики внес английский философ Ф.Бэкон (1561 – 1626), создавший индуктивную логику. Дальнейшее развитие логика получает в французской и немецкой философских школах.

Логические учения в Украине начинают распространяться со второй половины XV в. и получают развитие в Киево-Могилянской академии. В XIX в. выходят логические сочинения П. Д. Лодия и А. А. Потебни.

Второй период в развитии логики ознаменовался существенными изменениями, связанными с формированием математической или символической логики. Символическая логика – это результат применения математических методов к логике. Используя формализованный язык символов и формул, символическая логика изучает мышление в особых формально–логических системах. Это логика по предмету и математика по методу.

Заслуга в разработке символической логики принадлежит английским логикам Дж. Булю, У. С. Джевонсу, Дж. Венну, немецкому логику Э. Шредеру, американскому философу и логику Ч. Пирсу и русскому математику П. С. Порецкому и др. Классическую форму символическая логика получила в работах английского философа Б. Рассела.

Логика как наука изучает человеческое мышление, рассматривая его как орудие, средство познания окружающего мира и его свойств. При этом логика сосредотачивает внимание не на всех аспектах мышления, а лишь на том, в каких формах оно протекает и каким законам подчиняется. Поэтому логика – это философская наука о формах и законах правильных рассуждений и доказательств.

Логика и язык

Законы и формы мышления, изучаемые логикой – это идеальные объекты, которые обнаруживают себя лишь в языке путем специального анализа языковых форм. Использование формализованного языка позволяет в различных национальных языках обнаружить общую языковую структуру мыслей и обмен достижениями логики в различных странах.

Связь языка и мышления предполагает выявление логических структур и логических форм посредством анализа языка.

Язык – это система знаков, служащая средством человеческого общения и мышления и в своей основе конструируется при помощи знаков. Знак – это материальный, чувственно воспринимаемый объект, который символически, условно представляет и отсылает к обозначенному им предмету, явлению или свойству и сигнализирует о них. Знаки языка изучаются наукой – семиотикой (греч. semeiotos – обозначенный). Семиотика – это общая теория, исследующая знаковые системы, а также естественные и искусственные языки. Основоположником семиотики является американский философ, математик, логик Чарльз Пирс (1839 – 1914).

Семиотика анализирует язык в трех аспектах: синтаксическом, семантическом и прагматическом. Ч. Пирс разделил все знаки на три вида: знаки – образы, знаки – символы и знаки – индексы. Как и другие науки, логика широко использует искусственный символический язык с целью более точной и экономной передачи информации.

Язык символической логики – это формализованный язык, построение которого происходит на основе особой теории логического анализа, строго сформулированных правил и требует четкого описания его структуры и смысловых значений, которые задаются: а) исходными символами, составляющими алфавит языка логики; б) определением допустимых в языке выражений; в) семантической (т.е. смысловой) интерпретацией выражений и терминов.

В символической логике применяют две разновидности логического языка: язык логики высказываний (исчисление высказываний) и язык логики предикатов (исчисление предикатов).

Логика высказываний – это теория таких логических высказываний, которые не зависят от внутреннего строения простых высказываний. При этом логика высказываний исходит из двух допущений:

- анализирует высказывания, чтобы выяснить их логическое значение, т.е. определяет их истинность или ложность;

- что значение истинности сложного высказывания зависит от истинности значений простых высказываний, являющихся частями сложного высказывания и характера их связи.

Язык логики использует выражения, выполняющие функции двух видов: именные функции и пропозициональные функции. Именной функцией называют выражения, которые при замене их переменных постоянными, превращаются в обозначение предмета. Примеры: возьмем именные функции: «брат х»; «у - философ»; х² + 5. Поставив вместо Х «писатель Лев Толстой», получим «брат писателя Льва Толстого»; поставив вместо У «И.Кант», получим «И. Кант - философ», поставив вместо х² «5», получим «5² + 5». Таким образом, мы получили имена предметов.

Пропозициональной (от лат. proposition – предложение) функцией называется выражение, содержащее переменную и, которое превращается в истинное или ложное высказывание, если вместо переменной подставить имя предмета из определенной предметной области. Например: «х – город Украины», «у – основатель логики», «х + у = 15». Поставив вместо переменных Х и У имена предметов «Донецк», «Аристотель», «5 + 10», получим истинные суждения «Донецк – город Украины», «Аристотель – основатель логики», «5 + 10 = 15».

Логический анализ понятий и основных законов логики

Понятие как форма мышления представляет научный интерес для философии и логики. Если философия рассматривает понятия как учение о сущности в различных его проявлениях, как категорию, характеризующуюся динамической устойчивостью, как ступеньку процесса познания, то логика анализирует понятие как термин, отличающийся однозначностью. В логике термин – это имя для предметов универсума (т.е. предметной области в пределах научной теории), для обозначения субъекта и предиката суждения, а также элементов посылок силлогизма.

В традиционной логике учение о понятии составляет один из важнейших разделов, а в символической (классической) логике теория определения понятия, которая рассматривается с точки зрения построения формализованных языков. Понятию отводится роль пропозициональной функции предиката применительно к потребностям логических исчислений.

Специальный язык для выражения понятий и отношений между ними разработал немецкий философ и логик Готтлоб Фреге (1848 – 1925). Использование этого языка позволяет выявить связь структуры понятий со структурой суждений.

Логический аспект исследования понятий предполагает определение и анализ логических операций с ними. Формирование понятий в процессе познания связано с выделением общих и существенных признаков предметов и явлений. Признаки предметов не очевидны, их нужно отыскать. Для этого используют логические методы сравнения, анализа и синтеза, абстрагирования и обобщения.

Сравнением называют метод, при котором устанавливается сходство или различие между рассматриваемыми предметами и явлениями. С помощью сравнения выявляются количественные и качественные характеристики предметов, происходит их классификация и оценка. Поэтому сравнение сопровождает умственную и практическую деятельность людей. Сравнение только тогда дает правильные выводы, когда соблюдаются следующие правила: 1) сравниваются только однородные предметы; 2) сравниваются предметы по существенным и необходимым признакам.

Сравнение должно сочетаться с такими логическими методами, как анализ и синтез.

Анализ (греч. слова analysis – разложение, расчленение) – это логический метод, при котором изучаемый предмет мысленно или практически расчленяется на части или элементы, затем каждая из них изучается в отдельности. Процесс анализа сопровождается образованием суждений о существенных свойствах изучаемых частей. Формально-логический анализ связан с уточнением логической формы (структуры, строения) рассуждения и его составных частей: понятий, суждений, умозаключений. Анализ – это движение познания от внешнего к внутреннему, существенному.

Анализ органически связан с синтезом (греч. слова syntasis – соединение, сочетание). Это мысленное или практическое соединение расчлененного для анализа предмета, установление взаимодействия этих частей и познание его уже как целого. Синтез ведет к образованию понятий и тем самым дает новые знания.

Синтез включает в себя логический прием – абстрагирование. Абстрагирование (лат. abstraktio – удаление, отвлечение) – это мысленное выделение основных признаков, составляющих содержание понятия и одновременное отвлечение от других признаков. Результатами абстрагирования являются отвлеченные понятия. Процесс абстрагирования подчиняется следующим законам: 1) требование полноты абстракции; 2) абстракция имеет предел, определяемый предметом исследования.

В процессе логического мышления, связанного с определением понятия, абстрагирование является одним из моментов, тесно связанным с обобщением. Обобщение – это логический метод, при котором делается общий вывод о принадлежности данного признака целому классу предметов. Обобщение есть многоактный процесс, при котором происходит переход от единичного к общему, от менее общего к более общему понятию. Таким образом, в результате использования указанных приемов, мы получаем определенное понятие, как мысленное отражение предметов и явлений в форме обобщенного единства общих и существенных признаков.

Понятие и множество. Теория понятия пересекается с теорией множеств, так как множество заданное каким-либо условием, представляет собой объем данного понятия. Логика оперирует понятиями: «множество», «подмножество», «элемент». Основоположником теории множеств является немецкий математик, логик и философ Георг Кантор (1845-1918). Согласно Г. Кантору, множество – любое собрание определенных и различимых между собой объектов нашей интуиции или интеллекта, мыслимое как единое целое. Например, множество точек на прямой, множество городов Украины. Множество обозначают буквой «М» (от первой буквы немецкого слова «Menge» - множество), а его элементы заключают в фигурные скобки: М= {а, б, с, d}. Объекты, входящие в данное множество, называются его элементами, их принято обозначать строчными буквами: а, в, с, … x, y, z. Множество может включать в себя подмножество как его часть. Так, множество студентов Донецкой области являются частью (подмножеством) множества студентов Украины. Отношения между ними выражаются так: обозначим буквой А – множество студентов Украины, буквой В – множество студентов Донецкой области. Используя символ отношения «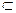», получим: В 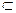А. Обозначив элемент буквой «а» - г. Донецк, и буквой «С» - города Донецкой области, мы можем выразить их отношение символически: а 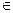С. 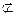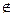Если данное подмножество или элемент не принадлежат множеству, то зачеркиваем символ принадлежности: В А; а С.

Различают универсальное, единичное, пустое, конечное и бесконечное множества. Символически их обозначают следующим образом: универсальное – «U», графически . Точки внутри прямоугольника будут элементами универсального множества. Единичное множество - {а}, пустое Ø. Существует два способа задания множества. Конечное множество задается путем перечисления элементов и записывается символически. Например, А – множество основных законов логики, тогда А = {а, б, с, d}. При задании бесконечного множества, мы выделяем свойство (признак), присущее каждому элементу. Например, множество простых чисел {2, 3, 5, 7 … }. Для элементов этого множества характерна делимость на единицу и на самого себя. Символическая запись такова: М= {Х/Р(Х)}. Читается так: множество всех чисел Х обладает свойством Р, т.е. делимостью на единицу и на самого себя. Два множества между собой равны, если они имеют равное число элементов.

Виды понятий. В зависимости от содержания, отображенного в понятии, они делятся на виды: родовые и видовые, общие и единичные, регистрируемые и нерегистрируемые, конкретные и абстрактные, безотносительные и соотносительные, положительные и отрицательные. Знание видов понятий необходимо и важно для проведения логических операций с ними, их классификации и логической характеристики. Например, дадим логическую характеристику понятию «студент». Это понятие конкретное, общее, положительное, нерегистрирующее, а понятие «храбрость» - абстрактное, общее, положительное, нерегистрирующее и соотносительное (соотноситься с понятием «трусость»).

Содержание и объем понятий. Всякое понятие имеет содержание и объем. Совокупность существенных признаков, отраженных в данном понятии, составляет его содержание. Например, содержанием понятия «товар» будут признаки: быть продуктом труда, иметь стоимость и удовлетворять потребность покупателя. Совокупность всех предметов, отраженных в данном понятии, образуют его объем. Объем понятия «товар» включает все товары, которые были, есть и будут. Поэтому его объем бесконечен. Тогда как объем месяцев года ограничен числом 12, а объем понятия «г. Донецк» состоит из одного элемента. Как видим объемы понятий различаются в зависимости от объекта отражения.

Содержание и объем понятия диалектически взаимосвязаны и одно без другого не существуют. Эта их взаимосвязь позволяет устанавливать отношения между ними, которые подчиняются закону обратного отношения между содержанием и объемом. Закон гласит: увеличение содержания понятия ведут к образованию понятия с меньшим объемом и наоборот. Например: «студент → студент Украины → студент Украины в Донецкой области → студент ДонНУЭТ». Такая логическая операция, когда от понятия с большим объемом, но с меньшим содержанием, переходим к понятию с меньшим объемом, но с большим содержанием, в логике называется, ограничением понятия. Обратная операция, называется обобщением понятия. Пределом ограничения является единичное понятие, а пределом обобщения – философские категории.

Все множество понятий в логике делятся на два подмножества: сравнимые и несравнимые понятия. Сравнимыми называют понятия, в содержании которых имеются общие признаки. Например: понятия «книга» и «учебник» сравнимы, так как некоторые книги учебники, а некоторые учебники книги. Два понятия, в содержании которых нет общих признаков, называются несравнимыми. Например, понятия «человек» и «гора» несравнимы, так как нет общих признаков.

В логические отношения вступают только сравнимые понятия, которые делятся на совместимые и несовместимые понятия. В зависимости от наличия или отсутствия общих признаков эти виды понятий объединяют в различные варианты отношений совместимости. Совместимые понятия деляться на: 1) отношения равнозначности; 2) отношения пересечения; 3) отношения подчинения или субординации. Несовместимые делятся на: а) отношения соподчинения или координации; б) отношения противоположности или контрарности; в) отношения противоречивости или контрадикторности.

Отношения между понятиями по содержанию и объему принято изображать с помощью круговых схем (Эйлера-Венна). Это позволяет получить новые понятия. Круг обозначает объем понятия, а точки в круге – предметы, отраженные в понятии. Продемонстрируем отношения между понятиями с помощью круговых схем: отношения совместимости.

Рис. 1 выражает отношения равнозначности:

А – 1 час и В – 60 минут. Содержание этих понятий

различно, а объемы совпадают, поэтому не рисуем два

круга.

Рис. 1

Рис. 2. выражает отношения пересечения:

А – студент; В – спортсмен. Студент одновременно может

быть спортсменом, а спортсмен – студентом. Наличие

общих признаков позволяет им пересекаться, поэтому

Рис. 2 заштрихованная часть схемы – это студенты – спортсмены.

Рис. 3. выражает отношения подчинения. Возьмем понятия

«космическое тело» и «планета». А- космическое тело, а В

планета. Планета – вид космического тела, поэтому

входит в объем космического тела, как в объем родового

понятия. В отношениях подчинения родовое понятие

будет подчиняющим, а видовое подчиненным.

Рис. 3

Отношения несовместимости: 1) отношения соподчинения

изображены на рис. 4. Обозначим А – человек, В –

мужчина, С – женщина. В объем родового понятия

«человек» входят видовые понятия «мужчина» и

«женщина».

Рис. 4. Помимо общих признаков у видовых понятий есть

признаки присущие только им и отсутствующие у общего,

родового понятия. 2) отношение противоположности

изображены на рис. 5. Понятие А – цвет, В – красный цвет,

С – зеленый цвет.

Рис. 5

Понятия В и С – противоположны. Объемы видовых

понятий «красный» и «зеленый» составляют лишь часть

объема родового понятия «цвет».

Отношения противоречия представлены на рис. 6. А – студент;

не – А – не студент. В сумме они составляют объем родового понятия «молодой человек».

Как видим, устанавливая отношения между понятиями, мы получаем не только новые понятия, но и новые знания о них.

Определение понятий. В символической логике

уделяется серьезное внимание теории определения

Рис. 6 понятий. Этой проблеме уделялось внимание еще в античной

философии. Прекрасными примерами являются сочинения Платона и, в особенности, «Метафизика» Аристотеля. Великолепным образцом использования логических операций определения и доказательства являются сочинения Б. Спинозы.

Определение (от лат. definition) - это логический прием, позволяющий формировать критерий отличия изучаемого объекта от других объектов. Так как результаты определения отражаются в понятиях, эти определения в некоторых случаях рассматриваются как формулировка в сжатой форме основного содержания понятий.

Никакое научное исследование не обходится без определений, так как это важнейшая часть научной теории. Чтобы определить понятие нужно решить две задачи: раскрыть содержание понятия (т.е. выявить его существенные признаки); отличить предмет, отраженный в понятии от сходных с ним предметов. Логическая операция, при которой выявляются существенные и отличительные признаки определенного понятия и тем самым раскрывается его содержание, называется определением.

В логике выработаны правила определения понятий. Рассмотрим правило, которое наиболее часто используется в научных исследованиях. Это правило гласит: понятие должно определяться через ближайший род и видовое отличие. Например, чтобы определить понятие «человек», нужно найти родовое (т.е. более широкое по объему) понятие. Таким понятием будет понятие «животное». Теперь найдем признаки, которые присущи только человеку. Этими признаками будут: язык как звуковая речь, сознание и умение создавать орудия труда. Получим: «Человек – это животное, обладающее языком, сознанием и умением создавать орудия труда».

Все определения делятся на явные и неявные. Определение через ближайший род и видовое отличие относятся к явным и характеризуются двумя частями. Первая часть называется Definiendum (лат. – определяемое) – это понятие, которое нужно определить. Вторая часть называется Definience (лат. – определяющее) – это понятие, с помощью которого дается определение. Согласно первому правилу Dfd º Dfn или формулу А = Вс, где А – определяемое понятие, Вс – определяющее (В – родовое понятие, С – отличительный признак, º -тождество).

Второе правило: определение не должно содержать в себе круга; третье – определение не должно быть отрицательным; четвертое – определение не должно содержать в себе противоречия; пятое – определение не должно быть двусмысленным; шестое – в качестве определяющего понятия нельзя брать литературные метафоры. Например: дети – цветы жизни.

Логические законы. Мышление человека подчиняется логическим законам, так как они носят нормативный и повелительный характер. Логические законы сформировались в сознании в результате наблюдения многократных процессов природы, общественной и практической деятельности, причем тех форм и способов деятельности, которые миллионы раз повторялись и откладывались в сознании как устойчивые связи. Логические законы объективны по своему содержанию и не зависят от воли человека, поэтому этим законам подчиняется процесс мышления всех людей.

В классической логике выделяется четыре основных закона: закон тождества, закон противоречия, закон исключенного третьего и закон достаточного основания. Первые три закона были исследованы и сформулированы Аристотелем. Четвертый закон сформулировал Лейбниц (1646 – 1716).

Основные законы классической логики применимы и в символической логике и, следует иметь в виду, что в символической логике применяются и другие законы. Например: закон двойного отрицания: а ® а; закон контрапозиции: (р ® g) º (g ® p); закон коммутативности дизъюнкции: (р Ú g) º (р Ú g) и т.д.

В символической логике законы называют тождественно – истинными формулами, так как при всех наборах значений для входящих в них переменных принимают значение истины.

Изучая логические законы, следует учесть, что эти законы выводного знания, так как это знания, полученные из ранее открытых и проверенных истин.

Переходя к изучению отдельных законов, отметим, что их изучение по отдельности осуществляется с целью достижения чистоты и глубины постижения их сущности. Анализируя отдельные законы, будем помнить, что Логический закон мышления – это необходимая, существенная и соответствующая действительности и правильно построенная связь между мыслями в процессе рассуждения.

Закон тождества. Согласно этому закону каждая мысль, которая приводится в суждении или умозаключении, при повторении должна иметь одно и то же определение и устойчивое содержание. Это значит, что всякая мысль в процессе рассуждения должна быть тождественна самой себе. Рассуждая о чем-либо, значения понятий и утверждений нельзя изменять, иначе свойства одного объекта будут приписаны другому объекту.

В символической логике закон тождества выражается формулой а = а; р ® р. Читается «а есть а», «р влечет р». Закон предъявляет два требования к мышлению: нельзя отождествлять различные мысли; нельзя тождественные мысли принимать за нетождественные.

Эти требования в процессе рассуждения нередко нарушаются по следующим причинам: 1). Любая мысль, излагаемая в языке, может быть выражена разными выражениями. Например: «г.Донецк» и «столица Донбасса». 2).Употребление многозначных слов, слов-омонимов. Именно на употреблении многозначных слов строятся различные софизмы. 3). Отождествление различных мыслей может произойти и от того, что люди разной профессии и жизненного опыта вкладывают в одно и то же понятие различный смысл.

Отождествление различных мыслей приводит к логической ошибке, которая называется подменой понятий. Эти ошибки следует избегать.

Закон противоречия. Наши суждения в процессе познания не должны противоречить друг другу. Закон противоречия гласит: Не могут быть одновременно истинными два противоположных суждения об одном и том же предмете, взятом в одно и то же время, в одном и том же отношении. Одно из этих суждений необходимо ложно. Противоречат друг другу суждения: «Студент Ткаченко сдал первую сессию на «отлично»» и «Студент Ткаченко не сдал первую сессию на «отлично»».

В символической логике закон выражается формулой «аÙа» или ù (р Ù ù р). Читается: «неверно, что р и не – р». Здесь буквы «а» или «р» означают любое высказывание, знак «Ù» - союз «И», а символы «ù» и «–» отрицание, т.е. «Не» или «Неверно, что», а – длинная черта над формулой – отрицание всей формулы, соединенной союзом «И».

Закон противоречия действует в отношении всех несовместимых суждений: контрарных (от лат. contraries – противоположный) и контрадикторных (от лат. contradictories – противоречащий). Закон этот анализирует два вида отношений между суждениями: отношения между противоположными и противоречащими суждениями. Отношения между этими видами суждений существенно отличаются. Суть их в следующем: отношения между контрарными суждениями такое, что вместе они не могут быть истинными. Если одно суждение истинно, то другое ложно, но если одно суждение ложно, то второе не обязательно истинно, оно также может быть ложным. Пример: «Все менеджеры имеют высшее образование» и «Ни один менеджер не имеет высшего образования». Эти суждения противоположны и, как видим, оба ложны.

Отношения между противоречащими суждениями таковы, что оба они не могут быть ни истинными, ни ложными. Если одно из них истинно, то другое непременно ложно и наоборот.

Закон исключенного третьего. Согласно этому закону истинно само высказывание или его отрицание. Например, «Киев – столица Украины» или «Киев – не столица Украины». Как видим, закон устанавливает связь только между противоречащими суждениями. Сущность закона формулируется так: два противоречащих суждения не могут быть одновременно ложными и одновременно истинными: одно из них необходимо истинно, а другое ложно.

Мы рассуждаем по формуле: «или – или», а третьего не дано. Символическая формула закона такова «аÚā». Читается «Истинно или а или отрицание а» (т.е. не – а; ā). Закон не допускает противоречия в мышлении. Если одно из противоречащих суждений истинно, то не нужно уклоняться от признания ложности другого и искать нечто третье. Значение закона и в том, что он указывает направление в отыскании истины и говорит, что возможны лишь два решения, а третье исключено.

Закон достаточного основания. Изучая законы логики, мы стремимся усвоить такие способы рассуждений, которые ведут нас к истине. Но мысль может быть истинной только тогда, когда она обоснована. Обосновать мысль, значит доказать ее соответствие действительности. Требование обоснованности и доказанности нашей мысли выражено в законе достаточного обоснования. Формулируется этот закон так: всякая мысль признается истинной, если она имеет достаточное обоснование.

Формула этого закона: А®В, если А, то В. Если вода нагрета до 100° по Цельсию, то она закипит. Готфрид Лейбниц, сформулировавший его, выразил это так: « Ни одно явление не может считаться истинным или действительным, ни одно утверждение справедливым без достаточного основания, почему дело обстоит именно так, а не иначе».

Среди множества способов обоснования истинности того или иного положения можно выделить следующие: личный опыт человека; соответствие выдвинутого положения установившимся в науке законам и теориям, подтвержденным фактами и практикой; проверка выдвинутого положения на возможность его эмпирического подтверждения или опровержения; проверка выдвинутого положения на то, распространяется ли оно на весь класс исследуемых объектов; согласуется ли данное утверждение с ранее принятыми. Если оно логически следует из них, то оно обосновано.

Таким образом, требование закона сводится к следующему: истинность выдвигаемого положения должна быть обоснована, что является важнейшим свойством научного мышления.