Физические свойства жидкостей

1. Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия, который определяется по формуле:

где V - первоначальный объем жидкости,

Величина обратная βV называется модулем объемной упругости жидкости:

Модуль объемной упругости не постоянен и зависит от давления и температуры. При гидравлических расчетах сжимаемостью жидкости обычно пренебрегают и считают жидкости практически несжимаемыми. Сжатие жидкостей в основном обусловлено сжатием растворенного в них газа.

2. Температурное расширение - относительное изменение объема жидкости при увеличении температуры на 1°С при Р = const. Характеризуется коэффициентом температурного расширения:

3. Сопротивление растяжению. Особыми физическими опытами было показано, что покоящаяся жидкость (в частности вода, ртуть) иногда способна сопротивляться очень большим растягивающим усилиям. Но в обычных условиях такого не происходит, и поэтому считают, что жидкость не способна сопротивляться растягивающим усилиям.

4. Силы поверхностного натяжения - эти силы стремятся придать сферическую форму жидкости. Силы поверхностного натяжения обусловлены поверхностными силами и направлены всегда внутрь рассматриваемого объема перпендикулярно свободной поверхности жидкости.

5. Вязкость жидкости - свойство жидкости сопротивляться скольжению или сдвигу ее слоев. Суть ее заключается в возникновении внутренней силы трения между движущимися слоями жидкости, которая определяется по формуле Ньютона:

μ- динамический коэффициент вязкости, или сила вязкостного трения,
d /dy - градиент скорости, перпендикулярный к поверхности сдвига.

Отсюда динамическая вязкость равна:

где τ - касательные напряжения жидкости

Величина обратная динамическому коэффициенту вязкости (1/μ) называется текучестью жидкости.

Отношение динамического коэффициента вязкости к плотности жидкости называется кинематическим коэффициентом вязкости:

Вязкость жидкости зависит от температуры и от давления. При повышении температуры вязкость жидкости уменьшается и наоборот.

3. рабочие жидкости.

Рабочая жидкость - жидкость, используемая как носитель энергии. В качестве рабочих жидкостей применяются минеральные, синтетические и полусинтетические масла, жидкости на силиконовой основе, водо-масляные эмульсии, масляно-водяные эмульсии.

Рабочие жидкости для гидросистем должны удовлетворять следующим требованиям:

-вязкостью в требуемом диапазоне значений;

-высоким индексом вязкости (минимальной зависимостью вязкости от температуры);

-хорошими смазывающими свойствами;

-химической инертностью к материалам, из которых сделаны элементы гидропривода;

-высоким объёмным модулем упругости;

-высокой устойчивостью к химической и механической деструкции;

-высоким коэффициентом теплопроводности и удельной теплоёмкости и малым коэффициентом теплового расширения;

-высокой температурой вспышки;

-нетоксичностью. Одна из функций рабочих жидкостей — защита деталей гидропривода от коррозии, поэтому рабочие жидкости обычно содержат антикоррозионные присадки. Другая функция рабочей жидкости — теплообмен между элементами гидросистемы, а также обмен теплом с окружающей средой. Также рабочие жидкости осуществляют надёжную смазку трущихся поверхностей деталей элементов гидросистемы.

4. Понятие о гидростатическом давлении и его свойствах

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

среднее гидростатическое давление, действующее на дно резервуара определяется по формуле:

где Р- сила, площадь дна – S

Гидростатическое давление обладает свойствами:

1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости. 2. Гидростатическое давление неизменно во всех направлениях.

3. Гидростатическое давление в точке зависит от ее координат в пространстве.

P=f(x, y, z)

5. Дифференциальное уравнение равновесия жидкости (уравнения Эйлера)

Уравнения гидростатика Эйлера (уравнения равновесия) определяют закон распределения давления в покоящейся жидкости вдоль соответствующей оси координат.

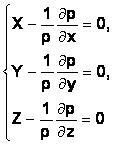
здесь X,Y,Z – напряжения массовых сил в проекциях на соответствующие оси координат x, y, z,

p – давление в соответствующей точке жидкости,

ρ - плотность жидкости.

Из уравнений Эйлера можно получить следующий вид основного диф-ного уравнения равновесия жидкости

Если ввести силовую (потенциальную) функцию U, такую, что

,

,

,

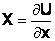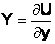то для несжимаемой жидкости дифференциальное уравнение равновесия примет вид:

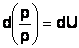
6. Диф. уравнение поверхности равного давления.

Дифференциальное уравнение поверхности равного давления выводится из дифференциального уравнения гидростатики (уравнение Эйлера)

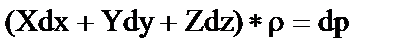
при p=const получается, что dp=0 и выражение в скобках равно нулю.

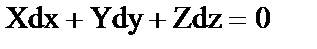, (1)

Где X, Y, Z - проекции равнодействующей (результирующей) массовой силы, отнесенной к единице массы жидкости, на соответствующие координатные оси (эти проекции равны соответствующим ускорениям);

dx, dy,dz - приращения (изменение) координат точек, составляющих поверхность равного давления.

В случае относительного равновесия жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью, на каждую частицу жидкости действуют две массовые силы: сила тяжести и центробежная сила инерции.

Рассмотрим в качестве поверхности равного давления свободную поверхность жидкости, в любой точке которого давление равно атмосферному. Отсюда получим:

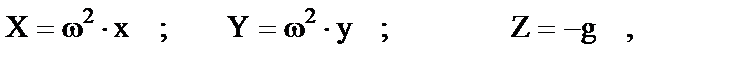гдеx, y - проекции радиуса вращения точки М на координатные оси;

ω - угловая скорость вращения.

Подставив найденные проекции в уравнение (1) и проинтегрировав его, получим:

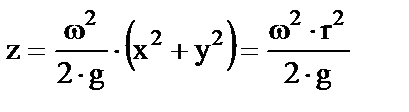(2)

Выражение (2) есть уравнение параболоида вращения, сечение которого горизонтальной плоскостью представляет окружность, а вертикальной плоскостью - параболу.

Из выражения (2) видно, что форма параболоида вращения не зависит от рода налитой в сосуд жидкости, ни от формы сосуда.

7. Понятие о вакуумном, абсолютном и манометрическом давлениях.

Если давление, измеряемое в точке ниже величины атмосферного давления, то раз­ница между замеренным давлением и атмосферным называется давлением вакуума

Абсолютное давление – это сумма избыточного или манометрического давления (показаний прибора измерения давления) и атмосферного Рабс = Ризб + Ратм

Абсолютное давление понимается как полное или истинное давление жидкости.

Абсолютное и вакуумное давления соотносятся следующим образом: Р_абс = Р_атм - Р_вак

Отсюда следует важное свойство вакуумного давления (вакуума) – абсолютное значение вакуумного давления не может быть больше атмосферного.

Если за уровень от­счёта принята величина атмосферного давления, то разница между абсолютным давлени­ем и атмосферным называется манометрическим давлением.

8. Приборы для измерения давления

Измерение давления необходимо для управления технологическими процессами и обеспечения безопасности производства. Кроме того, этот параметр используется при косвенных измерениях других технологических параметров: уровня расхода температуры, плотности и т. д. В системе СИ за единицу давления принят паскаль (Па).

Для измерения давления используют манометры, вакуумметры, мановакуумметры, напоромеры, тягомеры, тягонапоромеры, датчики давления, дифманометры.

В большинстве приборов измеряемое давление преобразуется в деформацию упругих элементов, поэтому они называются деформационными.

Деформационные приборы широко применяют для измерения давления при ведении технологических процессов благодаря простоте устройства, удобству и безопасности в работе. Все деформационные приборы имеют в схеме какой-либо упругий элемент, который деформируется под действием измеряемого давления: трубчатую пружину, мембрану или сильфон. Промышленность выпускает также мембранные дифманометры с промежуточными преобразователями, имеющими унифицированные токовые или пневматические сигналы.

Для измерения давления агрессивных сред применяют датчики, снабженные защитной мембраной, изготовленной, как и в дифманометрах, из коррозионно-стойкого материала. Измеряемое давление передается к измерительной мембране через силиконовое масло, которым заполнена внутренняя полость датчика.

10. Примеры относительного покоя жидкости

Под относительным покоем понимается такое состояние, при котором в движущейся жидкости отдельные частицы не смещаются одна относительно другой. При этом жидкость перемещается как твердое тело. Само движение жидкости в этом случае можно назвать переносным движением. Для этого состояния характерно постоянство формы объема жидкости.

На жидкость, находящуюся в относительном покое, действуют массовые силы (силы тяжести и силы инерции переносного движения), а из поверхностных — силы давления.

11. Условие плавания тел

Плавучесть тела - способность тела плавать в погруженном состоянии

остойчивость - наз. способность плавающего тела при отклонении в заданных пределах от положения равновесия возвращаться в начальное положение.

F_т>F_A - тело тонет; F_т=F_A - тело плавает в жидкости или газе; F_т<F_A - тело будет плавать в погруженном состоянииF_т- сила тяжестиF_{A -} Сила Архимеда

12.. Остойчивость тела Остойчивость тела - способность плавающего тела, выведенного из положения равновесия, возвращаться вновь к исходному положению после прекращения действия возмущающих сил.

Если для тела 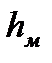>0 – то это судно является остойчивым

Если для тела 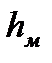<0 – такое судно не остойчиво

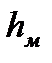-метацентрический радиус

13.. основные определения. Линия тока, трубка тока, элементарная струйка, элементарный расход.

Линией тока наз. линия в каждой точке которой в данное мгновение вектор скорости жидкости совпадает с направлением касательной к этой линии.

Л. т. могут быть найдены аналитически, если известны компоненты скорости потока в каждой точке 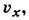i 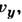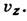В этом случае Л. т. получаются интегрированием дифференц. ур-ний Л. т.: 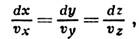Трубка тока - трубка, составленная из линий тока, проходящих через точки небольшого замкнутого контура внутри движущейся жидкости. Касательные к линиям тока совпадают с направлением скоростей движения частиц жидкости, находящихся на этих линиях. Элементарная струйка – совокупность линий тока, проведенных через все точки элементарной площадки. Элементарный расход - объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Таким образом: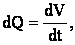

15. Характеристика ламинарного движения. Ламинарное течение — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления). Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Число ренольдца равно =V*d/υ,где V-средняя скорость,d-диаметр трубы,υ-кинематическая вязкость жидкости.Прит ламинарном движении Re_R < Re_Rкр, безразмерная величина .Ф-ла Дарси Вейсбоха.- эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях. 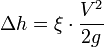гдеΔ h — потери напора на гидравлическом сопротивлении;ξ — коэффициент потерь

(коэффициент Дарси); V — средняя скорость течения жидкости; g — ускорение свободного падения; Формула Пуазёйля- При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости. hg= 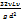= 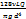где

L- длина трубки

V- Средняя скорость

Q-расход

d- Внутренний диаметр

g- Ускорение сил тяжести.Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле: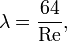

16. Характеристика турбулентного режима движения.Турбулентное течение, форма течения жидкости или газа, при которой их элементы совершают неупорядоченные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущихся жидкости или газа. Турбулентное течение отличаются от соответствующих ламинарных течений как своей сложной внутренней структурой, так и распределением осреднённой скорости по сечению потока и интегральными характеристиками — зависимостью средней по сечению или максимальной скорости, расхода, а также коэффициента сопротивления от Рейнольдса числа Re. При турбулентном режиме слоистость нарушается, движение жидкости сопровождается перемешиванием и пульсациями скорости и давления.Движение турбулентное если турбулентным, если _р; Re_R > Re_Rкр,В выражениях приведенных выше Re_кр и Re_Rкр — критические числа Рейнольдса. Число ренольдца равно =V*d/υ,где V-средняя скорость,d-диаметр трубы,υ-кинематическая вязкость жидкости. Формула Шези:V=C 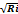или Q=wC 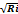гдеC- Коэффициент Шези R- Гидравлический радиус I- уклон дна V- Средняя скорость w- Площадь

18. Путевые и местные сопротивления

Путевые потери- распределяются по длине потока равномерно(при равномерном движении)или несколько неравномерно(при плавно изменяющимся неравномерном дви жении)

Местные потери,получающиеся только в отдельных местах потока,где поток претерпевает ту или другую резкую местную деформацию

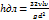– уравнение Пуазеля (при лам. движ.), 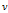- кинетич.к-т вязкости, l-длина трубопровода, 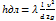- ф-ла Дарси-Вейсбаха; 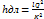при турбулентном движ.

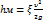- уравнение Вейсбаха, гдеξ-к-т местного сопротив.

Также путевые потери можно найти через ур-ие Бернули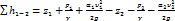

19. Виды насадок и области их применения

Насадки по форме патрубка могут быть цилиндрические внешние и внутренние, конические сходящиеся и расходящиеся и коноидальные, выполненные по форме выходящей струи.

Внешний цилиндрический насадок (насадок Вентури) применяется для увеличения пропускной способности отверстия в качестве водосбросных и дренажных труб

Внутренний цилиндрический насадок (насадок Борда) используется для опорожнения резервуаров, когда по конструктивным соображениям нельзя установить насадок Вентури.

Конически сходящийся насадок (конфузор) дает возможность получать компактную струю, обладающую большой кинетической энергией. Применяется в соплах гидравлических турбин, водоструйных и пароструйных насосах, гидромониторах, брандспойтах и т. д. Коэффициенты истечения для этих насадков зависят от угла конусности.

Конически расходящийся насадок (диффузор) применяется в эжекторных установках, в дымоходах, в аэродинамических трубах, дождевальных машинах, в каналах направляющего аппарата насосов, во всасывающих трубах насосов и турбин и т. д.

Коноидальный насадок имеет вход, выполненный по очертаниям выходящей из отверстия струи, поэтому потери при движении жидкости минимальны. Он позволяет почти в полтора раза увеличивать расход через отверстие, и выходящая струя обладает большой кинетической энергией.

24. .гидравлическое моделирование

Гидродинамическое подобие - это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.

Из геометрии известно, что геометрическое подобие означает про-порциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, поверхностей, которые ограничивают потоки жидкости, Таким образом в гидравлике геометрическое подобие означает подобие русел или трубопроводов, по которым течет жидкость. Кинематическое подобие это подобие линий тока и пропорциональность сходственных скоростей. Это значит, что для кинематического подобия потоков требуется соблюдение геометрического подобия.

Динамическое подобие заключается в пропорциональности сил, действующих на сходственные элементы кинематически и геометрически подобных потоков, и равенство углов, характеризующих направление действия этих сил. В потоках жидкостей обычно действуют разные силы – силы давления, силы вязкого трения, силы тяжести, инерционные силы. Соблюдение пропорциональности всех сил, действующих в потоке, означает полное гидродинамическое подобие. На практике полное гидродинамическое подобие достигается редко, поэтому обычно приходится ограничиваться частичным (неполным) гидродинамическим подобием, при котором имеется пропорциональность лишь основных сил. Записывается подобие следующим образом. Например, пропорциональность сил давления Р и сил трения Т, действующих в потоках I и II, можно записать в виде.

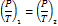
Критерии подобия для потоков несжимаемой жидкости

Критерий подобия Ньютона, Критерий подобия Рейнольдса, Критерий подобия Фруда

в подобных напорных потоках имеем равенство безразмерных коэффициентов и чисел α, δ, λ, Eu, Re, Ne. Изменение Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также несколько меняться. Поэтому все эти коэффициенты следует рассматривать как функции Re (хотя в некоторых интервалах Re они могут оставаться постоянными).

67.. Виды движения жидкости.

Различают 2 вида движения: установившееся и не установившееся.

Установившееся - такой вид движения при котором скорость. Ускорение, давление и глубины не изменяются с течением времени, а зависят только от положения в потоке жидкости рассматриваемой в точке являясь функцией координат.

u=f(x; y;z) – скорость частицы

P= f(x; y;z) – гидродинамическое давление

h= f(x; y;z) – глубина потока в данной точке.

Установшееся дв. разделяется на равномерное и не равномерное.

Равномерным движением наз такой вид установившегося движения при котором все компоненты движения скорость. Давление, форма русла, глубина меняются по направлению потока. Не равномерное дв – наблюдается в конической трубе, в которой по длине меняется поперечное сечение, а следовательно скорость и глубина.

Не установившееся дв – такой вид движения при котором все скорости, ускорения, давления, глубины являются функцией координат, но не времени.

Напорное дв –движение жидкости в потоке без свободной поверхности

Без напорное – движение жидкости когда поток не со всех сторон ограничен стенками, а имеет свободную поверхность.