Момент силы относительно точки и оси

Моментом силы относительно точки O называют величину, равную векторному произведению радиус-вектора 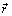, проведенного из точки O в точку приложения силы (рис. 2.1), на эту силу

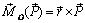. (2.1)

Этот вектор приложен в точке O и направлен перпендикулярно плоскости, содержащей векторы 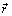и в ту сторону, откуда вращение тела, вызываемое силой вокруг точки O, представляется происходящим против часовой стрелки.

Модуль момента

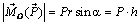, (2.2)

где 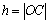– плечо силы относительно точки O, равное расстоянию от этой точки до линии действия силы . Из формулы (2.2) следует, что 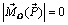, если h = 0, т.е. если линия действия силы проходит через точку О.

Обозначим через x, y, z координаты точки приложения силы, 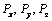– проекции силы на координатные оси. Тогда момент силы можно представить следующим образом

, (2.3)

откуда следует, что проекции момента силы на координатные оси равны

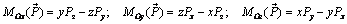. (2.4)

Моментом силы относительно оси называют величину, равную проекции на эту ось момента силы, взятого относительно некоторой точки оси

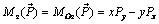. (2.5)

Момент силы относительно оси не зависит от выбора точки O на оси, так как ни одна из величин в правой части формулы (2.5) не зависит от положения начала координат при параллельном перемещении осей x и y.

Проекцией силы на плоскость называют вектор, начало и конец которого совпадают с проекциями начала и конца вектора силы на эту плоскость. На рис. 2.2 показана проекция силы на плоскость xОy. Так как проекции сил и , а также точек их приложения на оси x и y одинаковы, момент силы относительно точки O может быть вычислен по формуле (2.3), где следует положить, что z = 0 и ,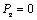

.

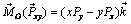Этот момент направлен вдоль оси z, а его проекция на эту ось совпадает с моментом силы относительно оси z:

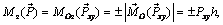
где h – плечо силы относительно точки O.

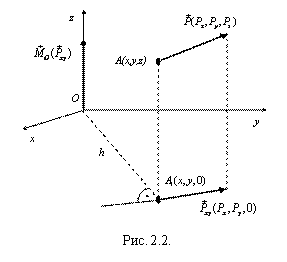
Таким образом, можно сформулировать следующее правило вычисления момента силы относительно оси z:

1) выберем на оси z произвольную точку и построим плоскость, перпендикулярную этой оси;

2) спроецируем силу на эту плоскость;

3) определим плечо проекции силы;

4) вычислим момент силы относительно оси z по формуле

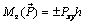. (2.6)

В формуле (2.6) знак «плюс» ставим в том случае, если с положительного направления оси z поворот тела вокруг этой оси виден направленным против часовой стрелки, знак «минус» – в противном случае. Аналогично вычисляют моменты силы относительно других координатных осей.

Из формулы (2.6) следует, что момент силы относительно оси равен нулю в двух случаях:

1) если сила параллельна оси, т.е. проекция = 0;

2) если линия действия силы пересекает ось, т.е. плечо h = 0.

Оба случая можно объединить: момент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось лежат в одной плоскости.